Semi-group of non-linear operators
A one-parameter family of operators 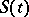 ,
, 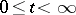 , defined and acting on a closed subset
, defined and acting on a closed subset 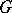 of a Banach space
of a Banach space 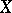 , with the following properties:
, with the following properties:
1) 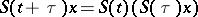 for
for  ,
, 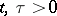 ;
;
2) 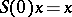 for any
for any 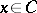 ;
;
3) for any 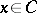 , the function
, the function 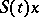 (with values in
(with values in 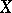 ) is continuous with respect to
) is continuous with respect to 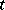 on
on  .
.
A semi-group 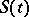 is of type
is of type 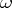 if
if
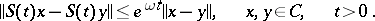 |
A semi-group of type  is called a contraction semi-group.
is called a contraction semi-group.
As in the case of semi-groups of linear operators (cf. Semi-group of operators), one introduces the concept of the generating operator (or infinitesimal generator) 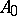 of the semi-group
of the semi-group 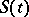 :
:
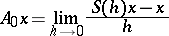 |
for those elements 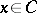 for which the limit exists. If
for which the limit exists. If 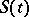 is a contraction semi-group,
is a contraction semi-group, 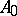 is a dissipative operator. Recall that an operator
is a dissipative operator. Recall that an operator 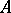 on a Banach space
on a Banach space  is dissipative if
is dissipative if  for
for 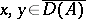 ,
, 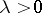 . A dissipative operator may be multi-valued, in which case
. A dissipative operator may be multi-valued, in which case 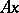 in the definition stands for any of its values at
in the definition stands for any of its values at  . A dissipative operator is said to be
. A dissipative operator is said to be 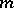 -dissipative if
-dissipative if 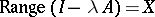 for
for 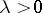 . If
. If 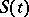 is of type
is of type 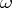 , then
, then 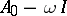 is dissipative.
is dissipative.
The fundamental theorem on the generation of semi-groups: If 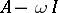 is a dissipative operator and
is a dissipative operator and 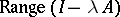 contains
contains 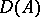 for sufficiently small
for sufficiently small  , then there exists a semi-group
, then there exists a semi-group 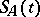 of type
of type 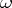 on
on 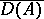 such that
such that
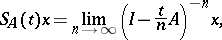 |
where 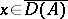 and the convergence is uniform on any finite
and the convergence is uniform on any finite 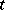 -interval. (The existence of
-interval. (The existence of 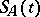 can also be proved if one replaces the condition
can also be proved if one replaces the condition 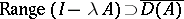 by the weaker condition
by the weaker condition
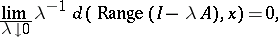 |
where 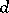 is the distance between sets.)
is the distance between sets.)
For any operator  one has a corresponding Cauchy problem
one has a corresponding Cauchy problem
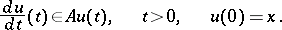 | (*) |
If the problem (*) has a strong solution, i.e. if there exists a function 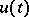 which is continuous on
which is continuous on 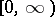 , absolutely continuous on any compact subset of
, absolutely continuous on any compact subset of 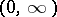 , takes values in
, takes values in 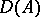 for almost all
for almost all 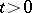 , has a strong derivative for almost all
, has a strong derivative for almost all 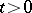 , and satisfies the relation (*), then
, and satisfies the relation (*), then 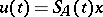 . Any function
. Any function 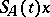 is a unique integral solution of the problem (*).
is a unique integral solution of the problem (*).
Under the assumptions of the fundamental theorem, if 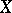 is a reflexive space and
is a reflexive space and 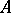 is closed (cf. Closed operator), then the function
is closed (cf. Closed operator), then the function 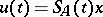 yields a strong solution of the Cauchy problem (*) for
yields a strong solution of the Cauchy problem (*) for 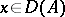 , with
, with 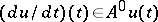 almost everywhere, where
almost everywhere, where 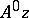 is the set of elements of minimal norm in
is the set of elements of minimal norm in 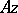 . In that case the generating operator
. In that case the generating operator 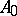 of the semi-group
of the semi-group 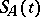 is densely defined:
is densely defined: 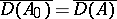 . If, moreover,
. If, moreover, 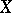 and
and 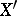 are uniformly convex, then the operator
are uniformly convex, then the operator 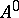 is single-valued and for all
is single-valued and for all 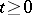 there exists a right derivative
there exists a right derivative 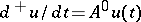 ; this function is continuous from the right on
; this function is continuous from the right on 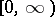 , and continuous at all points with the possible exception of a countable set; in this case
, and continuous at all points with the possible exception of a countable set; in this case 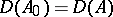 and
and 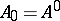 .
.
If 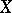 is reflexive (or
is reflexive (or 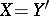 , where
, where 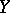 is separable) and
is separable) and 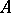 is a single-valued operator and has the property that
is a single-valued operator and has the property that  in
in 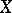 and
and 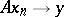 in the weak topology
in the weak topology 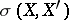 (respectively, in
(respectively, in 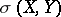 ) imply
) imply 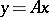 , then
, then  ,
, 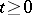 , and
, and 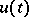 is a weakly (weak-
is a weakly (weak- ) continuously-differentiable solution of the problem (*). In the non-reflexive case, examples are known where the assumptions of the fundamental theorem hold with
) continuously-differentiable solution of the problem (*). In the non-reflexive case, examples are known where the assumptions of the fundamental theorem hold with 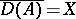 and the functions
and the functions  do not even have weak derivatives on
do not even have weak derivatives on 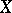 at any
at any 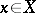 ,
,  .
.
Let 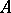 be a continuous operator, defined on all of
be a continuous operator, defined on all of 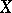 , such that
, such that  is dissipative. Then
is dissipative. Then 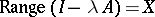 for
for 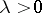 ,
, 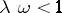 , and for any
, and for any  the problem (*) has a unique continuously-differentiable solution on
the problem (*) has a unique continuously-differentiable solution on 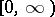 , given by
, given by 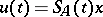 . If
. If 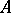 is continuous on its closed domain
is continuous on its closed domain 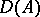 , then it will be the generating operator of a semi-group of type
, then it will be the generating operator of a semi-group of type 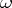 on
on 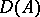 if only and only if
if only and only if 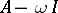 is dissipative and
is dissipative and 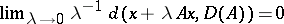 for
for 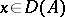 .
.
In a Hilbert space 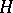 , a contraction semi-group on a set
, a contraction semi-group on a set 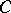 may be extended to a contraction semi-group on a closed convex subset
may be extended to a contraction semi-group on a closed convex subset 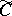 of
of 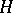 . Moreover, the generating operator
. Moreover, the generating operator 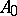 of the extended semi-group is defined on a set dense in
of the extended semi-group is defined on a set dense in 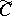 . There exists a unique
. There exists a unique 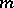 -dissipative operator such that
-dissipative operator such that 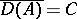 and
and 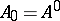 . If
. If 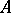 is
is 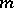 -dissipative, then
-dissipative, then 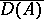 is convex and there exists a unique contraction semi-group
is convex and there exists a unique contraction semi-group  on
on 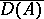 such that
such that 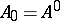 .
.
Let 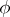 be a convex semi-continuous functional defined on a real Hilbert space
be a convex semi-continuous functional defined on a real Hilbert space 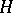 and let
and let 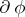 be its subdifferential; then the operator
be its subdifferential; then the operator 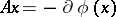 (for all
(for all  such that
such that 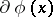 is non-empty) is dissipative. The semi-group
is non-empty) is dissipative. The semi-group 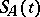 possesses properties similar to those of a linear analytic semi-group. In particular,
possesses properties similar to those of a linear analytic semi-group. In particular, 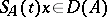 (
(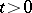 ) for any
) for any 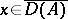 , and
, and 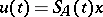 is a strong solution of the Cauchy problem (*), with
is a strong solution of the Cauchy problem (*), with
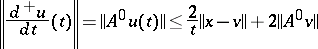 |
for all 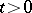 ,
, 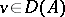 . If
. If 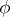 attains its minimum, then
attains its minimum, then 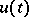 converges weakly to some minimum point as
converges weakly to some minimum point as 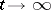 .
.
Theorems about the approximation of semi-groups play an essential role in the approximate solution of Cauchy problems. Let 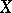 ,
,  ,
,  be Banach spaces; let
be Banach spaces; let 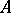 ,
, 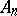 be operators defined and single-valued on
be operators defined and single-valued on 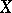 ,
, 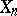 , respectively, satisfying the assumptions of the fundamental theorem for the same type
, respectively, satisfying the assumptions of the fundamental theorem for the same type 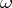 ; let
; let 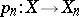 be linear operators,
be linear operators, 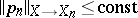 . Then convergence of the resolvents (cf. Resolvent) (
. Then convergence of the resolvents (cf. Resolvent) (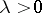 ,
, 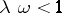 )
)
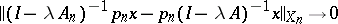 |
for 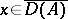 implies convergence of the semi-groups
implies convergence of the semi-groups
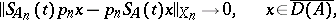 |
uniformly on any finite closed interval.
The multiplicative formulas developed by S. Lie in the finite-dimensional linear case can be generalized to the non-linear case. If 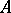 ,
, 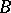 and
and 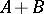 are single-valued
are single-valued 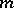 -dissipative operators on a Hilbert space and the closed convex set
-dissipative operators on a Hilbert space and the closed convex set 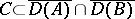 is invariant under
is invariant under 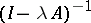 and
and 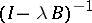 , then, for any
, then, for any 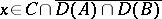 ,
,
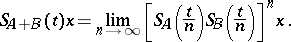 | (**) |
This formula is also valid in an arbitrary Banach space 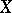 for any
for any 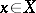 , provided
, provided 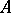 is a densely-defined
is a densely-defined 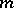 -dissipative linear operator and
-dissipative linear operator and 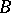 is a continuous dissipative operator defined on all of
is a continuous dissipative operator defined on all of 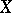 . In both cases
. In both cases
 |
 |
Examples of non-linear differential operators satisfying the conditions of the fundamental theorem on the generation of semi-groups are given below. In each case only the space  and the boundary conditions are indicated, while
and the boundary conditions are indicated, while 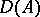 is not described. In all examples,
is not described. In all examples,  is a bounded domain in
is a bounded domain in 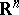 with smooth boundary;
with smooth boundary; 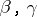 are multi-valued maximal monotone mappings
are multi-valued maximal monotone mappings 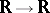 ,
, 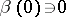 ,
, 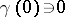 ; and
; and 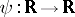 is a continuous strictly-increasing function,
is a continuous strictly-increasing function, 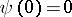 .
.
Example 1.
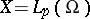 ,
, 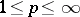 ,
, 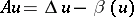 ,
,  on
on 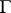 .
.
Example 2.
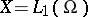 ,
, 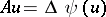 ,
, 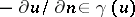 on
on 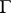 .
.
Example 3.
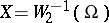 ,
,  ,
, 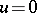 on
on 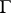 .
.
Example 4.
 or
or 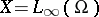 ,
, 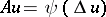 ,
,  on
on 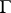 .
.
Example 5.
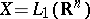 ,
, 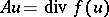 , where
, where 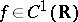 with values in
with values in 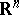 ,
, 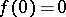 .
.
Example 6.
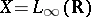 ,
, 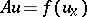 , where
, where 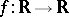 is continuous.
is continuous.
References
| [1] | V. Barbu, "Nonlinear semigroups and differential equations in Banach spaces" , Ed. Academici (1976) (Translated from Rumanian) |
| [2] | H. Brézis, "Opérateurs maximaux monotones et semigroups de contractions dans les espaces de Hilbert" , North-Holland (1973) |
| [3] | H. Brézis, A. Pazy, "Convergence and approximation of semigroups of nonlinear operators in Banach spaces" J. Funct. Anal. , 9 : 1 (1972) pp. 63–74 |
| [4] | M.G. Crandall, T.M. Liggett, "Generation of semi-groups of nonlinear transformations on general Banach spaces" Amer. J. Math. , 93 : 2 (1971) pp. 265–298 |
| [5] | Y. Kobayashi, "Difference approximation of Gauchy problems for quasi-dissipative operators and generation of nonlinear semigroups" J. Math. Soc. Japan , 27 : 4 (1975) pp. 640–665 |
| [6] | Y. Konishi, "On the uniform convergence of a finite difference scheme for a nonlinear heat equation" Proc. Japan. Acad. , 48 : 2 (1972) pp. 62–66 |
| [7] | R.H. Martin, "Differential equations on closed subsets of a Banach space" Trans. Amer. Math. Soc. , 179 (1973) pp. 399–414 |
| [8] | G.F. Webb, "Continuous nonlinear perturbations of linear accretive operators in Banach spaces" J. Funct. Anal. , 10 : 2 (1972) pp. 191–203 |
| [9] | M.I. [M.I. Khazan] Hazan, "Nonlinear evolution equations in locally convex spaces" Soviet Math. Dokl. , 14 : 5 (1973) pp. 1608–1614 Dokl. Akad. Nauk SSSR , 212 : 6 (1973) pp. 1309–1312 |
| [10] | M.I. [M.I. Khazan] Hazan, "Differentiability of nonlinear semigroups and the classical solvability of nonlinear boundary value problems for the equation 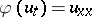 " Soviet Math. Dokl. , 17 : 3 (1976) pp. 839–843 Dokl. Akad. Nauk SSSR , 228 : 4 (1976) pp. 805–808 " Soviet Math. Dokl. , 17 : 3 (1976) pp. 839–843 Dokl. Akad. Nauk SSSR , 228 : 4 (1976) pp. 805–808 |
Comments
See also Semi-group of operators; One-parameter semi-group.
The formula (**) above, especially in the form
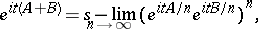 |
which holds, e.g., when 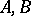 are self-adjoint operators on a separable Hilbert space so that
are self-adjoint operators on a separable Hilbert space so that 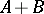 , defined on
, defined on 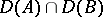 , is self-adjoint, is known as the Trotter product formula, [a5], [a4].
, is self-adjoint, is known as the Trotter product formula, [a5], [a4].
References
| [a1] | Ph. Clément, H.J.A.M. Heijmans, S. Angenent, C.J. van Duijn, B. de Pagter, "One-parameter semigroups" , CWI Monographs , 5 , North-Holland (1987) |
| [a2] | A. Pazy, "Semigroups of linear operators and applications to partial differential equations" , Springer (1983) |
| [a3] | R.H. Martin, "Nonlinear operators and differential equations in Banach spaces" , Wiley (1976) |
| [a4] | B. Simon, "Functional integration and quantum physics" , Acad. Press (1979) pp. 4–6 |
| [a5] | H. Trotter, "On the product of semigroups of operators" Proc. Amer. Math. Soc. , 10 (1959) pp. 545–551 |
Semi-group of non-linear operators. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Semi-group_of_non-linear_operators&oldid=48659