Self-adjoint differential equation
A linear ordinary differential equation 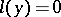 that coincides with the adjoint differential equation
that coincides with the adjoint differential equation 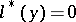 . Here
. Here
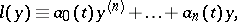 |
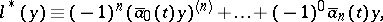 |
where
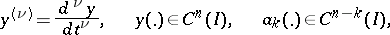 |
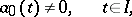 |
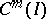 is the space of
is the space of 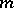 -times continuously-differentiable complex-valued functions on
-times continuously-differentiable complex-valued functions on 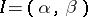 , and the bar denotes complex conjugation.
, and the bar denotes complex conjugation.
The left-hand side of every self-adjoint differential equation 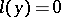 is a sum of expressions of the form
is a sum of expressions of the form
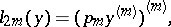 |
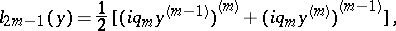 |
where 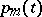 and
and 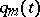 are sufficiently-smooth real-valued functions and
are sufficiently-smooth real-valued functions and 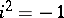 . A self-adjoint differential equation with real coefficients is necessarily of even order, and has the form
. A self-adjoint differential equation with real coefficients is necessarily of even order, and has the form
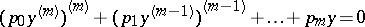 |
A linear system of differential equations
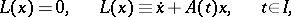 |
with a continuous complex-valued 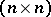 -matrix
-matrix 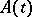 , is called self-adjoint if
, is called self-adjoint if 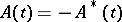 , where
, where 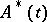 is the Hermitian conjugate of
is the Hermitian conjugate of 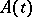 (see [1], [4], and Hermitian operator). This definition is not consistent with the definition of a self-adjoint differential equation. For example, the system
(see [1], [4], and Hermitian operator). This definition is not consistent with the definition of a self-adjoint differential equation. For example, the system
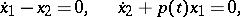 |
which is equivalent to the self-adjoint differential equation
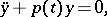 |
is self-adjoint as a linear system if and only if 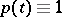 .
.
The boundary value problem
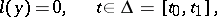 | (1) |
 | (2) |
where the 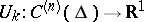 are linear and linearly independent functionals describing the boundary conditions, is called self-adjoint if it coincides with the adjoint boundary value problem, that is, (1) is a self-adjoint differential equation and
are linear and linearly independent functionals describing the boundary conditions, is called self-adjoint if it coincides with the adjoint boundary value problem, that is, (1) is a self-adjoint differential equation and 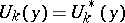 for all
for all 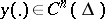 and for all
and for all 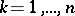 (see [1]–[3], [5]). If (1), (2) is a self-adjoint boundary value problem, then the equality (see Green formulas)
(see [1]–[3], [5]). If (1), (2) is a self-adjoint boundary value problem, then the equality (see Green formulas)
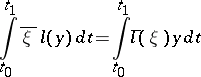 |
holds for any pair 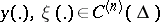 that satisfy the boundary conditions (2).
that satisfy the boundary conditions (2).
All the eigenvalues of the self-adjoint problem
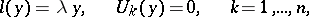 |
are real, and the eigenfunctions 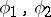 corresponding to distinct eigenvalues
corresponding to distinct eigenvalues 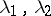 are orthogonal:
are orthogonal:
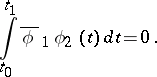 |
The linear boundary value problem
 | (3) |
where 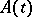 is a continuous complex-valued
is a continuous complex-valued 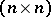 -matrix and
-matrix and 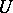 is an
is an  -vector functional on the space
-vector functional on the space 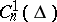 of continuous complex-valued functions
of continuous complex-valued functions 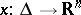 , is called self-adjoint if it coincides with its adjoint boundary value problem
, is called self-adjoint if it coincides with its adjoint boundary value problem
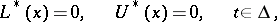 |
that is,
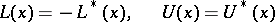 |
for all 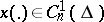 . A self-adjoint boundary value problem has properties analogous to those of the problem (1), (2) (see [4]).
. A self-adjoint boundary value problem has properties analogous to those of the problem (1), (2) (see [4]).
The concepts of a self-adjoint differential equation and of a self-adjoint boundary value problem are closely connected with that of a self-adjoint operator [6] (cf. also Spectral theory of differential operators). Self-adjointness and a self-adjoint boundary value problem are also defined for a linear partial differential equation (see [5], [7]).
References
| [1] | E. Kamke, "Differentialgleichungen: Lösungen und Lösungsmethoden" , 1. Gewöhnliche Differentialgleichungen , Chelsea, reprint (1971) |
| [2] | M.A. Naimark, "Linear differential operators" , 1–2 , Harrap (1968) (Translated from Russian) |
| [3] | E.A. Coddington, N. Levinson, "Theory of ordinary differential equations" , McGraw-Hill (1955) pp. Chapts. 13–17 |
| [4] | V.S. Vladimirov, "Equations of mathematical physics" , MIR (1984) (Translated from Russian) |
| [5] | P. Hartman, "Ordinary differential equations" , Birkhäuser (1982) |
| [6] | N. Dunford, J.T. Schwartz, "Linear operators. Spectral theory" , 2 , Interscience (1963) |
| [7] | V.P. Mikhailov, "Partial differential equations" , MIR (1978) (Translated from Russian) |
Comments
In general, the system of eigenfunctions is complete.
References
| [a1] | S. Agmon, "Lectures on elliptic boundary value problems" , v. Nostrand (1965) |
Self-adjoint differential equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Self-adjoint_differential_equation&oldid=48648