Self-adjoint differential equation

A linear ordinary differential equation 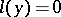that coincides with the adjoint differential equation 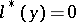. Here

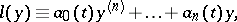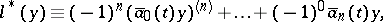where

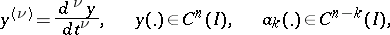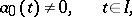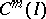is the space of 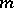-times continuously-differentiable complex-valued functions on 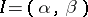, and the bar denotes complex conjugation.

The left-hand side of every self-adjoint differential equation 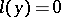is a sum of expressions of the form

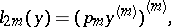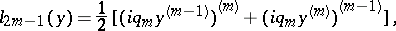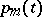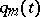where and are sufficiently-smooth real-valued functions and 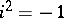. A self-adjoint differential equation with real coefficients is necessarily of even order, and has the form

(see [1]–[3]).

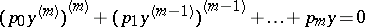A linear system of differential equations

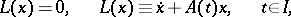with a continuous complex-valued 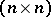-matrix 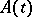, is called self-adjoint if 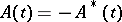, where 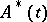is the Hermitian conjugate of 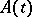(see [1], [4], and Hermitian operator). This definition is not consistent with the definition of a self-adjoint differential equation. For example, the system

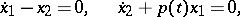which is equivalent to the self-adjoint differential equation

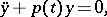is self-adjoint as a linear system if and only if .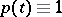

The boundary value problem

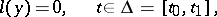(1)

(2)

where the 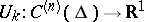are linear and linearly independent functionals describing the boundary conditions, is called self-adjoint if it coincides with the adjoint boundary value problem, that is, (1) is a self-adjoint differential equation and 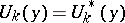for all 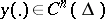and for all 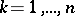(see [1]–[3], [5]). If (1), (2) is a self-adjoint boundary value problem, then the equality (see Green formulas)

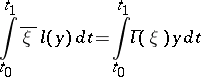holds for any pair 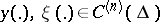that satisfy the boundary conditions (2).

All the eigenvalues of the self-adjoint problem

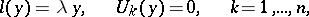are real, and the eigenfunctions 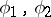corresponding to distinct eigenvalues 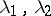are orthogonal:

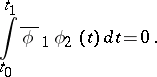The linear boundary value problem

(3)

where 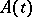is a continuous complex-valued 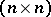-matrix and 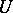is an -vector functional on the space 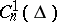of continuous complex-valued functions 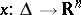, is called self-adjoint if it coincides with its adjoint boundary value problem

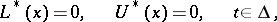that is,

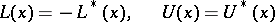for all 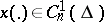. A self-adjoint boundary value problem has properties analogous to those of the problem (1), (2) (see [4]).

The concepts of a self-adjoint differential equation and of a self-adjoint boundary value problem are closely connected with that of a self-adjoint operator [6] (cf. also Spectral theory of differential operators). Self-adjointness and a self-adjoint boundary value problem are also defined for a linear partial differential equation (see [5], [7]).

References

[1]	E. Kamke, "Differentialgleichungen: Lösungen und Lösungsmethoden" , 1. Gewöhnliche Differentialgleichungen , Chelsea, reprint (1971)
[2]	M.A. Naimark, "Linear differential operators" , 1–2 , Harrap (1968) (Translated from Russian)
[3]	E.A. Coddington, N. Levinson, "Theory of ordinary differential equations" , McGraw-Hill (1955) pp. Chapts. 13–17
[4]	V.S. Vladimirov, "Equations of mathematical physics" , MIR (1984) (Translated from Russian)
[5]	P. Hartman, "Ordinary differential equations" , Birkhäuser (1982)
[6]	N. Dunford, J.T. Schwartz, "Linear operators. Spectral theory" , 2 , Interscience (1963)
[7]	V.P. Mikhailov, "Partial differential equations" , MIR (1978) (Translated from Russian)

Comments

In general, the system of eigenfunctions is complete.

References

[a1]	S. Agmon, "Lectures on elliptic boundary value problems" , v. Nostrand (1965)