Schauder method

A method for solving boundary value problems for linear uniformly-elliptic equations of the second order, based on a priori estimates and the continuation method (see also Continuation method (to a parametrized family)).

Schauder's method of finding a solution to the Dirichlet problem for a linear uniformly-elliptic equation

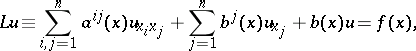(1)

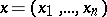given in a bounded domain of a Euclidean space of points and with a coefficient 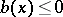, can be described in the following way.

1) The spaces , 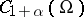and 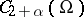are introduced as sets of functions 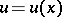with finite norms

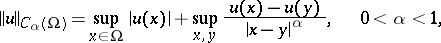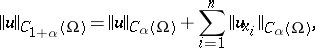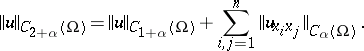2) It is assumed that the boundary of the domain is of class 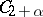, i.e. each element 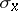of the 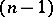-dimensional surface can be mapped on a part of the plane by a coordinate transformation 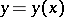with a positive Jacobian, moreover, .

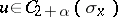3) It is proved that if the coefficients of (1) belong to the space 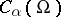and if the function 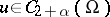, then the a priori estimate

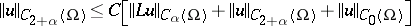(2)

is true up to the boundary, where the constant 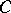depends only on , on the ellipticity constant 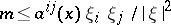, , 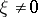and on the norms of the coefficients of the operator 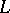, and where

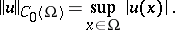4) It is assumed that one knows how to prove the existence of a solution 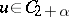to the Dirichlet problem

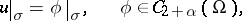for the Laplace operator .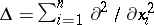

5) Without loss of generality one may assume that 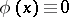, and then apply the continuation method, the essence of which is the following:

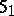. The operator 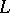is imbedded in a one-parameter family of operators

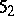. Basing oneself essentially on the a priori estimate (2), it can be established that the set 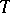of those values of 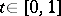for which the Dirichlet problem 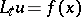, , 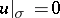has a solution for all 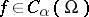, is at the same time open and closed, and thus coincides with the unit interval .

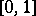6) It is proved that if 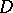is a bounded domain contained in together with its closure, then for any function and any compact subdomain 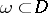the interior a priori estimate

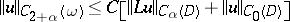(3)

holds.

7) Approximating uniformly the functions 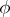and 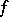by functions from 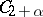and applying the estimate (3), one proves the existence of a solution to the Dirichlet problem for any continuous boundary function and for a wide class of domains with non-smooth boundaries, e.g. for domains that can be represented as the union of sequences of domains 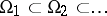, with boundaries of the same smoothness as .

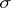Estimates 2 and 3 where first obtained by J. Schauder (see [1], [2]) and go under his name. Schauder's estimates and his method have been generalized to equations and systems of higher order. The a priori estimates, both interior and up to the boundary, corresponding to it are sometimes called Schauder-type estimates. The method of a priori estimates is a further generalization of Schauder's method.

References

[1]	J. Schauder, "Ueber lineare elliptische Differentialgleichungen zweiter Ordnung" Math. Z. , 38 : 2 (1934) pp. 257–282
[2]	J. Schauder, "Numerische Abschätzungen in elliptischen linearen Differentialgleichungen" Studia Math. , 5 (1935) pp. 34–42
[3]	L. Bers, F. John, M. Schechter, "Partial differential equations" , Interscience (1964)
[4]	R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , 2 , Interscience (1965) (Translated from German)
[5]	A.V. Bitsadze, "Some classes of partial differential equations" , Gordon & Breach (1988) (Translated from Russian)
[6]	Yu.M. [Yu.M. Berezanskii] Berezanskiy, "Expansion in eigenfunctions of selfadjoint operators" , Amer. Math. Soc. (1968) (Translated from Russian)
[7]	O.A. Ladyzhenskaya, N.N. Ural'tseva, "Linear and quasilinear elliptic equations" , Acad. Press (1968) (Translated from Russian)

Comments

Schauder-type estimates for parabolic equations were obtained for the first time in [a1] (see also [a2] for a detailed description).

References

[a1]	C. Ciliberto, "Formule di maggiorazione e teoremi di esistenza per le soluzioni delle equazioni paraboliche in due variabili" Ricerche Mat. , 3 (1954) pp. 40–75
[a2]	A. Friedman, "Partial differential equations of parabolic type" , Prentice-Hall (1964)
[a3]	D. Gilbarg, N.S. Trudinger, "Elliptic partial differential equations of second order" , Springer (1977)