Scalar curvature

of a Riemannian manifold at a point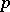

The trace of the Ricci tensor with respect to the metric tensor 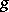. The scalar curvature 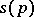is connected with the Ricci curvature and the sectional curvature 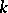by the formulas

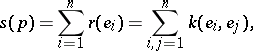where is an orthonormal basis of the tangent space. In the equivalent Einstein notation, these equations have the form

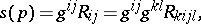where 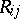and 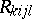are the components of the Ricci tensor and the curvature tensor, respectively, and the 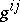are the contravariant components of the metric tensor.

References

[1]	D. Gromoll, W. Klingenberg, W. Meyer, "Riemannsche Geometrie im Grossen" , Springer (1968)
[2]	P.K. [P.K. Rashevskii] Rashewski, "Riemannsche Geometrie und Tensoranalyse" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian)

References

[a1]	S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , 1–2 , Interscience (1963–1969)