Saddle point method

A method for computing the asymptotic expansion of integrals of the form

(*)

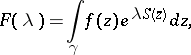where , is a large parameter, is a contour in the complex -plane, and the functions and are holomorphic in a domain containing . The zeros of 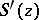are called the saddle points of 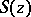. The essence of the method is as follows. The contour 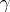is deformed to a contour 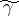with the same end-points and lying in 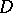and such that 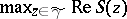is attained only at the saddle points or at the ends of 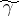(the contour of steepest descent). The asymptotics of the integral (*) along the path of steepest descent are calculated by means of the Laplace method and are equal to the sum of the contributions from the saddle points. The contribution 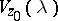from the point 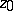is an integral of the form of (*) taken over a small arc of 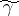containing the point 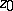. If 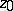is an interior point of 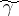and 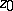is a saddle point with 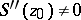, then

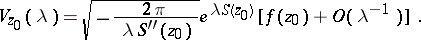The contour of steepest descent has a minimax property; on it,

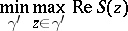is attained, where the minimum is taken over all contours 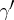lying in 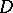having the same end-points as . The main difficulty in using the method is to select the saddle points, i.e. to choose the 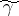corresponding to .

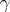The method is due to P. Debye [1], although the ideas in the method were suggested earlier by B. Riemann [2]. See [3]–[9] for the calculation of the contributions from the saddle points and from the end-points of the contour.

The method is in essence the only method for calculating the asymptotic expansions of integrals of the form (*). It can be used to derive the asymptotic expansions for Laplace, Fourier and Mellin transforms, as well as for transforms of exponentials of polynomials and many special functions.

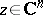Let , let 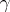be a bounded manifold with boundary of dimension and of class 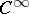, let functions 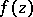and 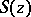be holomorphic in a certain domain 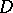containing , and let 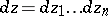. Suppose that 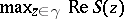is attained at a single point 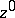which is an interior point for 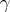and a non-singular saddle point for 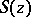, i.e. . Then the contribution from 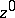is

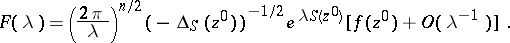References

[1]	P. Debye, "Näherungsformeln für die Zylinderfunktionen für grosse Werte des Arguments und unbeschränkt veranderliche Werte des Index" Math. Ann. , 67 (1909) pp. 535–558
[2]	B. Riemann, "Mathematische Werke" , Dover, reprint (1953)
[3]	A. Erdélyi, "Asymptotic expansions" , Dover, reprint (1956)
[4]	N.G. de Bruijn, "Asymptotic methods in analysis" , Dover, reprint (1981)
[5]	M.A. Evgrafov, "Asymptotic estimates and entire functions" , Gordon & Breach (1962) (Translated from Russian)
[6]	E.T. Copson, "Asymptotic expansions" , Cambridge Univ. Press (1965)
[7]	F.W.J. Olver, "Asymptotics and special functions" , Acad. Press (1974)
[8]	E.Ya. Riekstyn'sh, "Asymptotic expansions of integrals" , 1–2 , Riga (1974–1977) (In Russian)
[9]	M.V. Fedoryuk, "The saddle-point method" , Moscow (1977) (In Russian)

References

[a1]	R. Wong, "Asymptotic approximations of integrals" , Acad. Press (1989)