Rotation theorems

Theorems which characterize the change in the argument under a conformal mapping. Rotation theorems in the class 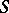of functions 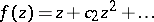which are regular and univalent in the disc 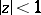give accurate estimates of the argument of the derivative for functions of this class:

(*)

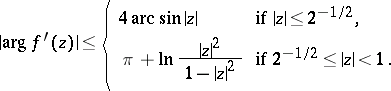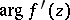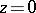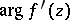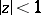Here one considers the branch of that vanishes when . The upper and the lower bounds for given by the inequalities (*) are sharp for any in the disc . This rotation theorem was obtained by G.M. Goluzin [1], [5]; I.E. Bazilevich [2] was the first to show that the inequalities (*) are sharp for 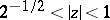; J.A. Jenkins [3] gave a complete analysis of the cases of equality in these estimates.

Rotation theorems in the class 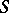is also the name given to estimates of 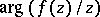and to estimates of expressions of the type

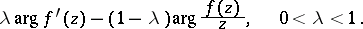The simplest estimates of this type in the class 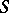are the sharp inequalities (the appropriate branches of the arguments are considered):

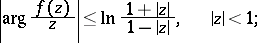There are also rotation theorems in other classes of functions which realize a univalent conformal mapping of the disc or its exterior, and in classes of functions which are univalent in a multiply-connected domain (cf. [5], [3], Distortion theorems; Univalent function). Rotation theorems have also been extended to include the case of 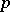-valued functions (cf. addenda to [5], and also Multivalent function).

References

[1]	G.M. Goluzin, "On distortion theorems in the theory of conformal mappings" Mat. Sb. , 1 (43) : 1 (1936) pp. 127–135 (In Russian) (German abstract)
[2]	I.E. Bazilevich, "Sur les théorèmes de Koebe–Bieberbach" Mat. Sb. , 1 (43) : 3 (1936) pp. 283–292
[3]	J.A. Jenkins, "Univalent functions and conformal mapping" , Springer (1958)
[4]	H. Grunsky, "Neue Abschätzungen zur konformen Abbildung ein- und mehrfach zusammenhängender Bereiche" Schriftenreihe Math. Sem. Inst. Angew. Math. Univ. Berlin , 1 (1932) pp. 95–140
[5]	G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian)

Comments

For the class 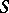see also Bieberbach conjecture.

References

[a1]	P.L. Duren, "Univalent functions" , Springer (1983) pp. Sect. 10.11