Rodrigues formula

A formula relating the differential of the normal to a surface to the differential of the radius vector of the surface in the principal direction:

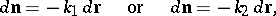where and are the principal curvatures.

The formula was obtained by O. Rodrigues (1815).

A.B. Ivanov

A representation of orthogonal polynomials in terms of a weight function using differentiation. If a weight function satisfies a Pearson differential equation

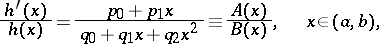and if, moreover, at the end points of the orthogonality interval the following conditions hold:

then the orthogonal polynomial can be represented by a Rodrigues formula:

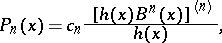where 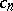is a constant. Rodrigues' formula holds only for orthogonal polynomials and for polynomials obtained from the latter by linear transformations of the argument. Originally, this formula was established by O. Rodrigues [1] for the Legendre polynomials.

References

[1]	O. Rodrigues, "Mémoire sur l'attraction des spheroides" Correspondence sur l'Ecole Polytechnique , 3 (1816) pp. 361–385

P.K. Suetin

Comments

For part 1) see also [a1], [a2]. For part 2) see also [a3], [a4].

References

[a1]	G. Darboux, "Leçons sur la théorie générale des surfaces et ses applications géométriques du calcul infinitésimal" , 1–4 , Chelsea, reprint (1972)
[a2]	M.P. Do Carmo, "Differential geometry of curves and surfaces" , Prentice-Hall (1976) pp. 145
[a3]	G. Szegö, "Orthogonal polynomials" , Amer. Math. Soc. (1975)
[a4]	T.S. Chihara, "An introduction to orthogonal polynomials" , Gordon & Breach (1978)