Rigged manifold
framed manifold
A smooth manifold with a fixed trivialization of the normal bundle. More accurately, let a smooth  -dimensional manifold
-dimensional manifold 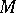 be imbedded in
be imbedded in  and let the (
and let the ( -dimensional) normal fibration
-dimensional) normal fibration  corresponding to this imbedding be trivial. Any trivialization of the fibration
corresponding to this imbedding be trivial. Any trivialization of the fibration  is called a rigging (framing) of the manifold
is called a rigging (framing) of the manifold 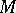 corresponding to this imbedding. Framed manifolds were introduced around 1950 (see [1]) in order to prove that the cobordism groups of
corresponding to this imbedding. Framed manifolds were introduced around 1950 (see [1]) in order to prove that the cobordism groups of  -dimensional framed manifolds lying in
-dimensional framed manifolds lying in  are isomorphic to the homotopy groups
are isomorphic to the homotopy groups  ; the groups
; the groups 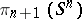 and
and  have been computed along these lines.
have been computed along these lines.
References
| [1] | L.S. Pontryagin, "Smooth manifolds and their application in homotopy theory" Trudy Mat. Inst. Steklov. , 45 (1955) (In Russian) |
Comments
The phrase "framed manifold" is also used to denote a differentiable manifold together with a basis in each fibre 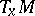 of its tangent bundle, with the chosen basis depending differentiably on
of its tangent bundle, with the chosen basis depending differentiably on  .
.
The frame bundle  over an
over an  -dimensional smooth manifold
-dimensional smooth manifold 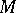 is the
is the  -dimensional smooth fibre bundle over
-dimensional smooth fibre bundle over 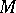 (so its total space is of dimension
(so its total space is of dimension 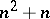 ) whose fibre over
) whose fibre over 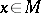 consists of all linear isomorphisms
consists of all linear isomorphisms 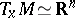 . Equivalently, the fibre at
. Equivalently, the fibre at  consists of all ordered bases, also called frames, for
consists of all ordered bases, also called frames, for  . Thus, more precisely, a framed manifold is a pair
. Thus, more precisely, a framed manifold is a pair 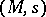 consisting of a smooth manifold
consisting of a smooth manifold 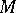 together with a section
together with a section 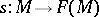 of the frame bundle. Such a section is called a framing.
of the frame bundle. Such a section is called a framing.
Quite generally, of course, the word "frame" is used as a substitute for basis in a vector space. The terminology derives from the fact that a basis in space-time provides a frame of reference in the sense of mechanics.
References
| [a1] | J.W. Milnor, "Toplogy from the differentiable viewpoint" , Univ. Virginia Press (1965) |
| [a2] | J.W. Milnor, "A survey of cobordism theory" L'Enseign. Math. , 8 (1962) pp. 16–23 |
| [a3] | R. Thom, "Quelque propriétés globales des variétés différentiables" Comm. Math. Helvet. , 28 (1954) pp. 17–28 |
| [a4] | J. Dieudonné, "A history of algebraic and differential topology 1900–1960" , Birkhäuser (1989) |
| [a5] | C.T.J. Dodson, "Categories, bundles, and spacetime topology" , Kluwer (1988) pp. 94ff |
| [a6] | M.W. Hirsch, "Differential topology" , Springer (1976) pp. 98 |
Rigged manifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rigged_manifold&oldid=48571