Riemannian curvature

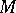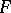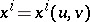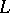A measure of the difference between the metrics of a Riemannian and a Euclidean space. Let be a point of a Riemannian space and let be a two-dimensional regular surface passing through , let be a simply closed contour in 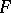passing through , and let be the area of the part of 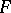bounded by 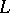. Apply the parallel displacement along 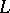to an arbitrary vector 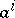tangent to 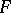(that is, a linear expression in the vectors 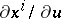, 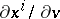). Then the component of the transferred vector tangential to 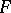turns out to be turned in relation to 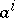by an angle 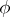(the positive reference direction of the angle must coincide with the direction of movement along ). If, when 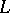is contracted to the point 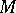, the limit

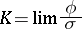exists, then it is called the Riemannian curvature (the curvature of the Riemannian space) at the given point in the direction of the two-dimensional surface; the Riemannian curvature does not depend on the surface but only on its direction at , that is, on the direction of the two-dimensional tangent plane to the Euclidean space that contains the vectors , .

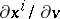The Riemannian curvature 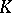is connected with the curvature tensor by the formula:

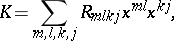where

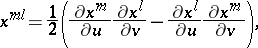in which the parameters 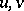are chosen such that the area of the parallelogram constructed on the vectors 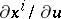, 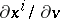equals 1.

Comments

The Riemannian curvature is better known as the sectional curvature.

For references see Riemann tensor.