Riemann function
The Riemann function in the theory of trigonometric series is a function introduced by B. Riemann (1851) (see [1]) for studying the problem of the representation of a function by a trigonometric series. Let a series
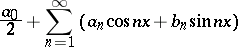 | (*) |
with bounded sequences 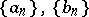 be given. The Riemann function for this series is the function
be given. The Riemann function for this series is the function  obtained by twice term-by-term integration of the series:
obtained by twice term-by-term integration of the series:
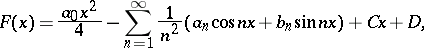 |
 |
Riemann's first theorem: Let the series (*) converge at a point 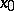 to a number
to a number 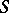 . The Schwarzian derivative (cf. Riemann derivative)
. The Schwarzian derivative (cf. Riemann derivative) 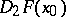 then equals
then equals 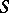 . Riemann's second theorem: Let
. Riemann's second theorem: Let 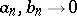 as
as 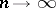 . Then at any point
. Then at any point  ,
,
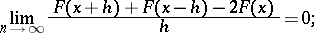 |
moreover, the convergence is uniform on any interval, that is, 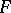 is a uniformly smooth function.
is a uniformly smooth function.
If the series (*) converges on  to
to 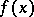 and if
and if 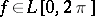 , then
, then 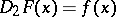 for each
for each 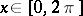 and
and
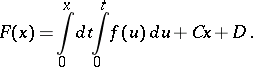 |
Let 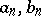 be real numbers tending to
be real numbers tending to  as
as 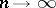 , let
, let
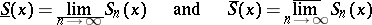 |
be finite at a point  , and let
, and let
 |
Then the upper and lower Schwarzian derivatives 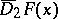 and
and 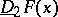 belong to
belong to 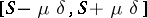 , where
, where  is an absolute constant. (The du Bois-Reymond lemma.)
is an absolute constant. (The du Bois-Reymond lemma.)
References
| [1] | B. Riemann, "Ueber die Darstellbarkeit einer Function durch eine trigonometrische Reihe" , Gesammelte Math. Abhandlungen , Dover, reprint (1957) pp. 227–264 |
| [2] | N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian) |
Comments
See also Riemann summation method.
For Riemann's function in the theory of differential equations see Riemann method.
Riemann function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Riemann_function&oldid=48546