Repeated limit

A limit of a function of several variables in which the passage to the limit is performed successively in the different variables. Let, for example, a function 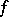of two variables and be defined on a set of the form 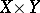, , 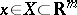, 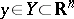and let 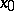and 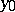be limit points of the sets 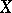and , respectively, or the symbol 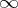(if or 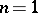, 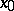and, respectively, 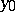may be infinities with signs: 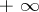, 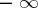). If for any fixed 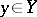the limit

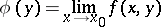(1)

exists, and for 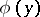the limit

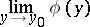exists, then this limit is called the repeated limit

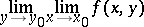(2)

of the function 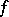at the point 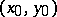. Similarly one defines the repeated limit

(3)

If the (finite or infinite) double limit

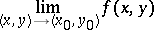(4)

exists, and if for any fixed 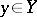the finite limit (1) exists, then the repeated limit (2) also exists, and it is equal to the double limit (4).

If for each 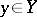the finite limit (1) exists, for each 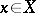the finite limit

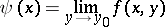exists, and for 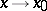the function 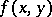tends to a limit function 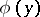uniformly in 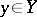, then both the repeated limits (2) and (3) exist and are equal to one another.

If the sets 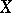and 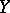are sets of integers, then the function 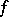is called a double sequence, and the values of the argument are written as subscripts:

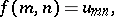and the repeated limits

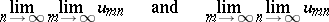are called the repeated limits of the double sequence.

The concept of a repeated limit has been generalized to the case where 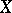and 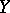and the set of values of the function 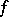are subsets of certain topological spaces.