Repeated integral

An integral in which there is a successive integration with respect to different variables, i.e. an integral of the form

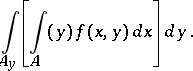(1)

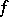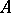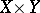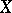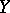The function is defined on a set lying in the direct product of spaces and in which are given 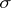-finite measures and 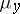and which have the completeness property; the set 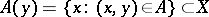(the "section" at "level" 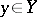of 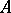) is measurable with respect to 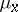, while the set 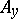(the projection of 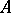on 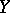) is measurable with respect to 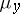. The integration over 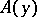is performed with respect to 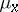, and that over 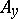with respect to 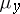. The integral (1) is also denoted by

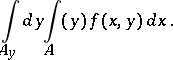Multiple integrals (cf. Multiple integral) can be reduced to repeated integrals.

Let a function 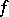, integrable with respect to the measure 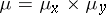on the set 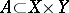, be extended by zero to a function on the entire space 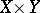. Then the repeated integrals

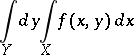and

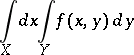exist and are equal to each other:

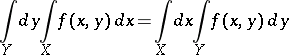(2)

(see Fubini theorem). In the left-hand integral the outer integration is in fact performed over the set 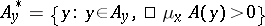. In particular, for points 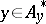the sets 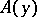are measurable with respect to . In general, one cannot take this integral over the entire set 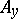since, while the set A is measurable with respect to 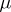, the set 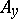may be non-measurable with respect to 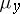, and similarly, the individual sets 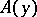, , 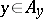may be non-measurable with respect to 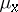. On the other hand, the set is always measurable with respect to 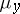provided only that the set 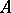is measurable with respect to .

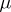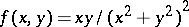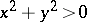The above conditions for changing the order of integration in a repeated integral are only sufficient but not necessary; sometimes it is permissible to change the order of integration in a repeated integral while the corresponding multiple integral does not exist. For example, for the function for and 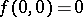the repeated integrals are equal:

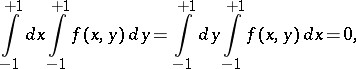while the multiple integral

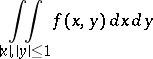does not exist. However, if at least one of the integrals

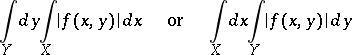is finite, then the function 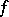is integrable on the set 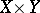and relation (2) holds.

In the case where the inner integral is a Stieltjes integral and the outer one is a Lebesgue integral, the following theorem on changing the order of integration holds: Let a function 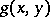be summable with respect to 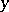in 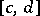for all values of in 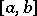and let it be a function of bounded variation with respect to in 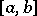for almost-all values 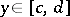. Also, suppose that the total variation of 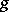with respect to the variable in 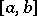for all given values of 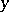does not exceed some non-negative summable function on 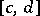. Then the function 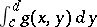is a function of bounded variation with respect to the variable in 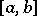and for any continuous functi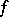on on one has the formula

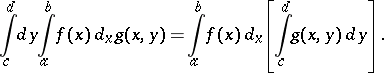References

[1]	V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , 1–2 , MIR (1982) (Translated from Russian)
[2]	A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian)
[3]	L.D. Kudryavtsev, "A course in mathematical analysis" , 2 , Moscow (1981) (In Russian)
[4]	S.M. Nikol'skii, "A course of mathematical analysis" , 2 , MIR (1977) (Translated from Russian)
[5]	V.I. Smirnov, "A course of higher mathematics" , 5 , Addison-Wesley (1964) (Translated from Russian)

Comments

Instead of "repeated integral" one also uses iterated integral (cf., e.g., [a1], [a2]).

References

[a1]	E. Hewitt, K.R. Stromberg, "Real and abstract analysis" , Springer (1965)
[a2]	W. Rudin, "Real and complex analysis" , McGraw-Hill (1978) pp. 24
[a3]	S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French)
[a4]	T.M. Apostol, "Mathematical analysis" , Addison-Wesley (1974)
[a5]	P.R. Halmos, "Measure theory" , Springer (1974)
[a6]	A.C. Zaanen, "Integration" , North-Holland (1974)