Radical of an ideal

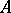in a commutative associative ring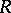

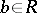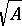The set of all elements some power of which is contained in . This set is denoted by . It is an ideal in 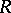; moreover, 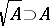and .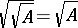

A generalization of this idea is that of the radical of a submodule. Let 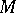be a module over 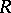and let 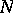be a submodule of 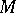. The radical of the submodule 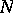is the set of all elements 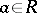such that 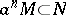for some integer (in general, depending on ). The radical of a submodule is an ideal in .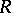

Comments

Consider the quotient ring 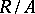and the natural quotient homomorphism 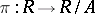. The radical of 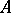is the inverse image of the nil radical (cf. Nil ideal) of .

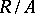Radical ideal is the phrase sometimes used to denote an ideal that is equal to its radical.

Let 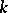be an algebraically closed field. To each ideal 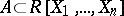one associates the algebraic set 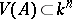, 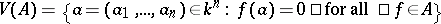. The Hilbert Nullstellensatz says that 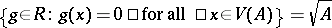. Thus there is in this setting a bijective correspondence between radical ideals and algebraic sets.

In the setting of affine schemes (cf. Affine scheme) 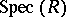this takes the following form. To each ideal 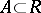one associates the closed subspace 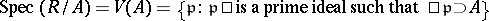. Conversely, to each closed subspace 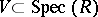one associates the ideal 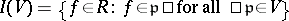. Then again 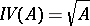because 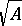is the intersection of all prime ideals containing 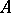, and, again, 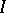and set up a bijective correspondence between radical ideals and closed subsets of 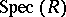. The difference with the setting of the Nullstellensatz is that in that case only prime ideals of the form 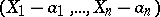are considered.

References

[a1]	P.M. Cohn, "Algebra" , II , Wiley (1977) pp. Sects. 11.2, 11.10
[a2]	A. Grothendieck, "Eléments de géométrie algébrique. I: Le language des schémas" Publ. Math. IHES , 20 (1960) pp. 80