Radical in a class of semi-groups
A function 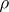 associating to each semi-group
associating to each semi-group 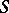 a congruence
a congruence 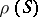 (cf. Congruence (in algebra)) and having the following properties: 1) if
(cf. Congruence (in algebra)) and having the following properties: 1) if 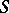 is isomorphic to
is isomorphic to 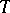 and
and 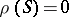 (0 denotes the equality relation), then
(0 denotes the equality relation), then  ; 2) if
; 2) if 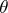 is a congruence on
is a congruence on 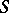 and
and 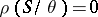 , then
, then 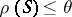 ; and 3)
; and 3)  . If 1) and 3) are satisfied, then 2) is equivalent to
. If 1) and 3) are satisfied, then 2) is equivalent to
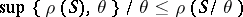 |
for every congruence 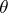 on
on 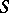 . A semi-group
. A semi-group 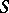 is called
is called 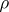 -semi-simple if
-semi-simple if 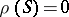 . The class of
. The class of  -semi-simple semi-groups contains the one-element semi-group and is closed relative to isomorphism and subdirect products. Conversely, each class of semi-groups having these properties is the class of
-semi-simple semi-groups contains the one-element semi-group and is closed relative to isomorphism and subdirect products. Conversely, each class of semi-groups having these properties is the class of 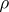 -semi-simple semi-groups for some radical
-semi-simple semi-groups for some radical 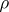 . If
. If 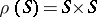 , then
, then 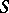 is called
is called 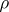 -radical. In contrast to rings, in semi-groups the radical is not determined by the corresponding radical class. If in the definition of a radical the discussion is limited to congruences defined by ideals, then another concept of a radical arises, where the corresponding function chooses an ideal in each semi-group.
-radical. In contrast to rings, in semi-groups the radical is not determined by the corresponding radical class. If in the definition of a radical the discussion is limited to congruences defined by ideals, then another concept of a radical arises, where the corresponding function chooses an ideal in each semi-group.
If 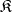 is a class of semi-groups that is closed relative to isomorphisms and that contains the one-element semi-group, then the function that associates to each semi-group
is a class of semi-groups that is closed relative to isomorphisms and that contains the one-element semi-group, then the function that associates to each semi-group 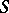 the intersection of all congruences
the intersection of all congruences 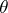 such that
such that 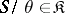 turns out to be a radical, called
turns out to be a radical, called 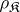 . The class
. The class 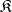 coincides with the class of
coincides with the class of 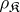 -semi-simple semi-groups if and only if it is closed relative to subdirect products. In this case
-semi-simple semi-groups if and only if it is closed relative to subdirect products. In this case  is the largest quotient semi-group of
is the largest quotient semi-group of 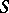 that lies in
that lies in 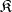 (see Replica).
(see Replica).
Example. Let 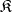 be the class of semi-groups admitting a faithful irreducible representation (cf. Representation of a semi-group). Then
be the class of semi-groups admitting a faithful irreducible representation (cf. Representation of a semi-group). Then
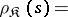 |
 |
where
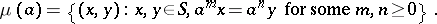 |
Radicals defined on a given class of semi-groups that is closed relative to homomorphic images have been studied.
Related to each radical  is the class of left polygons
is the class of left polygons  (cf. Polygon (over a monoid)). Namely, if
(cf. Polygon (over a monoid)). Namely, if  is a left
is a left  -polygon, then a congruence
-polygon, then a congruence  on
on  is called
is called  -annihilating if
-annihilating if  implies
implies 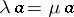 for all
for all 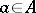 . The least upper bound of all
. The least upper bound of all  -annihilating congruences turns out to be an
-annihilating congruences turns out to be an 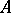 -annihilating congruence, and is denoted by
-annihilating congruence, and is denoted by  . The class
. The class 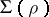 , by definition, consists of all left
, by definition, consists of all left 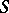 -polygons
-polygons 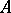 such that
such that  , where
, where 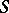 runs through the class of all semi-groups. If
runs through the class of all semi-groups. If 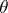 is a congruence on
is a congruence on 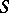 , then a left
, then a left 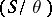 -polygon lies in
-polygon lies in  if and only if it lies in
if and only if it lies in 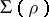 when considered as a left
when considered as a left 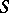 -polygon. Conversely, if one is given a class
-polygon. Conversely, if one is given a class 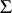 of left polygons with these properties and if
of left polygons with these properties and if 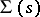 is the class of all left
is the class of all left 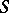 -polygons in
-polygons in 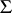 , then the function
, then the function
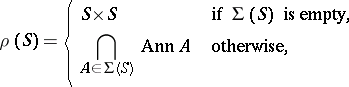 |
is a radical.
References
| [1] | A.H. Clifford, G.B. Preston, "The algebraic theory of semi-groups" , 2 , Amer. Math. Soc. (1967) |
| [2] | L.A. Skornyakov, "Radicals of  -rings" , Selected problems in algebra and logic , Novosibirsk (1973) pp. 283–299 (In Russian) -rings" , Selected problems in algebra and logic , Novosibirsk (1973) pp. 283–299 (In Russian) |
| [3] | A.H. Clifford, "Radicals in semigroups" Semigroup Forum , 1 : 2 (1970) pp. 103–127 |
| [4] | E.N. Roiz, B.M. Schein, "Radicals of semigroups" Semigroup Forum , 16 : 3 (1978) pp. 299–344 |
Radical in a class of semi-groups. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Radical_in_a_class_of_semi-groups&oldid=48413