Quotient object

of an object in a category

A concept generalizing the notions of a quotient set, a quotient group, a quotient space, etc.

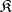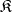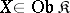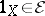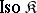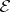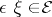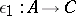Let be some class of epimorphisms in a category that contains all identity morphisms in and is closed under multiplication on the right by isomorphisms. In other words, for every , and for every in and every in the morphism . Two morphisms and in 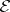are said to be equivalent if 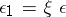for some isomorphism . The equivalence class of a morphism is called an 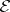-quotient object of the object 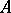, and the pair 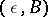is called a representative of the quotient object. A quotient object with representative 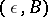is sometimes denoted by 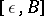, 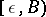or simply by .

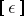Every object 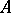has at least one 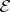-quotient object, the improper quotient object ; other quotient objects of 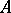are called proper. A category is called 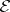-locally small if for every object 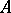in 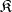the class of 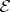-quotient objects of 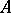is a set.

If one takes as 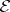the subcategory of all epimorphisms, 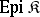, then 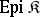-quotient objects are simply called quotient objects. If 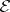is part of a bicategory structure 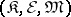on 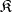, then 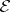-quotient objects are called admissible quotient objects. Similarly, if 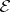consists of all regular (strict, normal, etc.) epimorphisms, then the corresponding quotient objects are called regular (strict, normal, etc). For example, in the category of topological spaces quotient spaces correspond to regular quotient objects.

The concept of a quotient object of an object in a category is dual to that of a subobject.

Comments

The terms "colocally small categorycolocally small" and "co-well-powered categoryco-well-powered" are often used instead of "locally small" .

References

[a1]	A. Grothendieck, "Sur quelques points d'algèbre homologique" Tohoku Math. J. , 9 (1957) pp. 119–221
[a2]	B. Mitchell, "Theory of categories" , Acad. Press (1965) pp. 7