Quasi-isometry

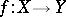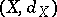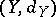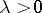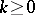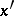A mapping , where and are metric spaces (cf. Metric space), for which there exist two constants and such that for all and in :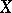

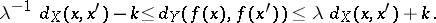This property expresses the fact that is "Lipschitz in the large" (cf. also Lipschitz constant). Such a mapping 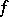is also called a 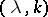-quasi-isometry.

Note that this definition, which is commonly used now (see [a1], §7.2.G), does not imply that is continuous. In [a4], §5.9, W. Thurston considers mappings satisfying the property above but with right-hand side replaced by 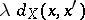. Such a mapping is continuous (cf. Continuous mapping) and Thurston calls it a pseudo-isometry. Some authors (see, e.g., [a3]) use the word quasi-isometry to denote a mapping having the property above, with the further condition that the image 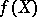is 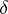-dense in 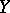, for some real number .

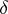The importance of quasi-isometries has been fully realized in the proof of Mostow's rigidity theorem [a2]. Thurston's lectures [a4] contain an excellent exposition of this theorem for manifolds of constant curvature .

References

[a1]	M. Gromov, "Hyperbolic groups" S.M. Gersten (ed.) , Essays in Group Theory , MSRI Publ. , 8 , Springer (1987) pp. 75–263
[a2]	G.D. Mostow, "Quasi-conformal mappings in -space and the strong rigidity of space-form" IHES Publ. Math. , 34 (1968) pp. 53–104
[a3]	P. Pansu, "Métriques de Carnot–Carathéodory et quasiisométries des espaces symétriques de rang un" Ann. of Math. , 129 : 1 (1989) pp. 1–61
[a4]	W. Thurston, "The geometry and topology of 3-manifolds" , Lecture Notes , Princeton Univ. Press (1976)