Quasi-equivalent representations
Two unitary representations (cf. Unitary representation)  of a group
of a group  (or symmetric representations of a symmetric algebra
(or symmetric representations of a symmetric algebra  ) in Hilbert spaces
) in Hilbert spaces  and
and  , respectively, satisfying one of the following four equivalent conditions: 1) there exist unitarily-equivalent representations
, respectively, satisfying one of the following four equivalent conditions: 1) there exist unitarily-equivalent representations  and
and  such that
such that  is a multiple of
is a multiple of  and
and  is a multiple of
is a multiple of  ; 2) the non-zero subrepresentations of
; 2) the non-zero subrepresentations of 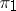 are not disjoint from
are not disjoint from  , and the non-zero subrepresentations of
, and the non-zero subrepresentations of  are not disjoint from
are not disjoint from  ; 3)
; 3) 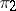 is unitarily equivalent to a subrepresentation of some multiple representation
is unitarily equivalent to a subrepresentation of some multiple representation  of
of  that has unit central support; or 4) there exists an isomorphism
that has unit central support; or 4) there exists an isomorphism  of the von Neumann algebra generated by the set
of the von Neumann algebra generated by the set  onto the von Neumann algebra generated by the set
onto the von Neumann algebra generated by the set  such that
such that  for all
for all  . Unitarily-equivalent representations are quasi-equivalent representations; irreducible quasi-equivalent representations (cf. Irreducible representation) are unitarily equivalent. If
. Unitarily-equivalent representations are quasi-equivalent representations; irreducible quasi-equivalent representations (cf. Irreducible representation) are unitarily equivalent. If 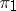 and
and 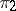 are quasi-equivalent representations and
are quasi-equivalent representations and  is a factor representation, then so is
is a factor representation, then so is  ; a factor representation and a non-zero subrepresentation of it are quasi-equivalent representations; two factor representations are either disjoint or quasi-equivalent. The notion of quasi-equivalent representations leads to that of a quasi-dual object and a quasi-spectrum for locally compact groups and symmetric algebras, respectively.
; a factor representation and a non-zero subrepresentation of it are quasi-equivalent representations; two factor representations are either disjoint or quasi-equivalent. The notion of quasi-equivalent representations leads to that of a quasi-dual object and a quasi-spectrum for locally compact groups and symmetric algebras, respectively.
References
| [1] | J. Dixmier, "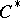 algebras" , North-Holland (1977) (Translated from French) algebras" , North-Holland (1977) (Translated from French) |
Comments
Two representations 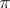 and
and  (of a group or algebra) with representation spaces
(of a group or algebra) with representation spaces  and
and  , respectively, are said to be disjoint is there is no non-zero intertwining operator between
, respectively, are said to be disjoint is there is no non-zero intertwining operator between  and
and  . Here, an intertwining operator between
. Here, an intertwining operator between  and
and 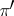 is a continuous linear operator
is a continuous linear operator  such that
such that 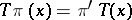 for all
for all  .
.
Quasi-equivalent representations. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quasi-equivalent_representations&oldid=48381