Prüfer domain
A commutative semi-hereditary integral domain (cf. also Semi-hereditary ring; Injective module). The Prüfer domains are the commutative integral domains  that satisfy the following two conditions:
that satisfy the following two conditions:
i) the localization 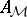 (cf. also Localization in a commutative algebra) is a valuation ring (see Valuation) for every maximal ideal
(cf. also Localization in a commutative algebra) is a valuation ring (see Valuation) for every maximal ideal 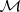 of
of 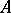 ;
;
ii) an 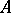 -module
-module 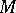 is flat (cf. Flat module) if and only if it is torsion-free (cf. also Group without torsion).
is flat (cf. Flat module) if and only if it is torsion-free (cf. also Group without torsion).
A Noetherian Prüfer domain is a Dedekind domain (see Dedekind ring). Each Bezout domain (also called Bezout ring) is a Prüfer domain.
There are Prüfer domains that are not Bezout and there are Prüfer domains having finitely generated ideals requiring more than two generators [a2] (hence, these are not Dedekind rings).
References
| [a1] | R. Gilmer, "Multiplicative ideal theory" , M. Dekker (1972) |
| [a2] | R. Heidman, L. Levy, "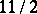 and and  -generator ideals in Prüfer domains" Rocky Mount. Math. J. , 5 (1975) pp. 361–373 -generator ideals in Prüfer domains" Rocky Mount. Math. J. , 5 (1975) pp. 361–373 |
| [a3] | H.C. Hutchins, "Examples of commutative rings" , Polygonal (1981) |
Prüfer domain. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pr%C3%BCfer_domain&oldid=48338