Projective transformation
A one-to-one mapping  of a projective space
of a projective space  onto itself preserving the order relation in the partially ordered (by inclusion) set of all subspaces of
onto itself preserving the order relation in the partially ordered (by inclusion) set of all subspaces of  , that is, a mapping of
, that is, a mapping of  onto itself such that:
onto itself such that:
1) if  , then
, then  ;
;
2) for every  there is an
there is an  such that
such that  ;
;
3)  if and only if
if and only if 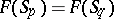 .
.
Under a projective transformation the sum and intersection of subspaces are preserved, points are mapped to points, and independence of points is preserved. The projective transformations constitute a group, called the projective group. Examples of projective transformations are: a collineation, a perspective and a homology.
Let the space 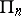 be interpreted as the collection of subspaces
be interpreted as the collection of subspaces 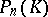 of the left vector space
of the left vector space 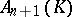 over a skew-field
over a skew-field 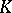 . A semi-linear transformation of
. A semi-linear transformation of 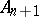 into itself is a pair
into itself is a pair 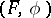 consisting of an automorphism
consisting of an automorphism  of the additive group
of the additive group 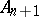 and an automorphism
and an automorphism  of the skew-field
of the skew-field  such that for any
such that for any  and
and  the equality
the equality 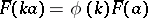 holds. In particular, a semi-linear transformation
holds. In particular, a semi-linear transformation 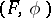 is linear if
is linear if 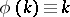 . A semi-linear transformation
. A semi-linear transformation  induces a projective transformation
induces a projective transformation 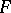 . The converse assertion is the first fundamental theorem of projective geometry: If
. The converse assertion is the first fundamental theorem of projective geometry: If 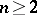 , then every projective transformation
, then every projective transformation 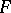 is induced by some semi-linear transformation
is induced by some semi-linear transformation  of the space
of the space  .
.
References
| [1] | R. Baer, "Linear algebra and projective geometry" , Acad. Press (1952) MR0052795 Zbl 0049.38103 |
| [2] | W.V.D. Hodge, D. Pedoe, "Methods of algebraic geometry" , 1 , Cambridge Univ. Press (1947) MR0028055 Zbl 0796.14002 Zbl 0796.14003 Zbl 0796.14001 Zbl 0157.27502 Zbl 0157.27501 Zbl 0055.38705 Zbl 0048.14502 |
Comments
A projective transformation can also be defined as a bijection of the points of  preserving collinearity in both directions.
preserving collinearity in both directions.
Other names used for a projective transformation are: projectivity, collineation. See also Collineation for terminology.
Projective transformation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Projective_transformation&oldid=48330