Primitive element in a co-algebra
Let  be a co-algebra over
be a co-algebra over  . An element
. An element  is called group like if
is called group like if  . An element
. An element  is called primitive over the group-like element
is called primitive over the group-like element  if
if  , [a2], p. 199. Let
, [a2], p. 199. Let  be a bi-algebra (see Hopf algebra) and let
be a bi-algebra (see Hopf algebra) and let  be the set of primitive elements over the group-like element
be the set of primitive elements over the group-like element 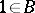 of
of  , considered as a co-algebra. Then
, considered as a co-algebra. Then 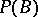 becomes a Lie algebra under the commutator bracket
becomes a Lie algebra under the commutator bracket
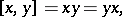 |
(using the multiplication of  ). This is the Lie algebra of primitive elements.
). This is the Lie algebra of primitive elements.
For 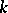 a field of characteristic zero, the functors
a field of characteristic zero, the functors  , the universal enveloping algebra of the Lie algebra
, the universal enveloping algebra of the Lie algebra 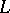 , and
, and 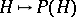 , where
, where 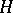 is a Hopf algebra (or bi-algebra) over
is a Hopf algebra (or bi-algebra) over  , establish an equivalence between the category of Lie algebras and the category of co-commutative irreducible bi-algebras (such bi-algebras are automatically Hopf algebras).
, establish an equivalence between the category of Lie algebras and the category of co-commutative irreducible bi-algebras (such bi-algebras are automatically Hopf algebras).
In particular, 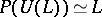 ,
, 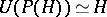 for such a bi-algebra (Hopf algebra) [a2], [a1]; for the graded version of this correspondence, see Hopf algebra and the references quoted there. See also Lie polynomial for the concrete case that
for such a bi-algebra (Hopf algebra) [a2], [a1]; for the graded version of this correspondence, see Hopf algebra and the references quoted there. See also Lie polynomial for the concrete case that 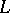 is a free Lie algebra (cf. Lie algebra, free) on a set
is a free Lie algebra (cf. Lie algebra, free) on a set 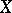 and
and 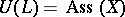 is the free associative algebra over
is the free associative algebra over 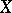 .
.
References
| [a1] | E. Abe, "Hopf algebras" , Cambridge Univ. Press (1977) |
| [a2] | M.E. Sweedler, "Hopf algebras" , Benjamin (1963) |
Primitive element in a co-algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Primitive_element_in_a_co-algebra&oldid=48284