Porosity point
of a set 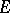 in a metric space
in a metric space 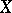
A point 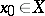 for which there exists a sequence of open balls
for which there exists a sequence of open balls 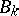 with radii
with radii 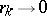 and common centre at the point
and common centre at the point 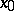 , such that for any
, such that for any 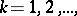 there is an open ball
there is an open ball 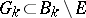 with radius
with radius 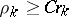 , where
, where 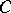 is positive and independent of
is positive and independent of 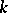 (but, generally speaking, depends on
(but, generally speaking, depends on 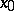 and
and  ). A set
). A set 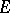 is called porous if any point in it is a porosity point of it. A set
is called porous if any point in it is a porosity point of it. A set 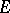 is called
is called 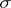 -porous if it can be represented as a finite or countable union of porous sets (see [1]). A porosity point of
-porous if it can be represented as a finite or countable union of porous sets (see [1]). A porosity point of 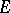 is a porosity point of its closure
is a porosity point of its closure 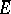 . If
. If 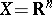 , a porosity point of a set
, a porosity point of a set 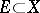 is not a Lebesgue density point either of
is not a Lebesgue density point either of 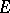 or of
or of 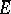 . Any porous or
. Any porous or 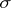 -porous set
-porous set 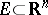 is of the first Baire category (cf. Baire classes) and of Lebesgue measure zero in
is of the first Baire category (cf. Baire classes) and of Lebesgue measure zero in 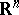 . The converse of this statement, generally speaking, does not hold: There even exist nowhere-dense perfect sets
. The converse of this statement, generally speaking, does not hold: There even exist nowhere-dense perfect sets 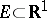 of measure zero that are not
of measure zero that are not 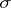 -porous (see [2]).
-porous (see [2]).
Sometimes, in the case of an infinite-dimensional space 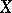 , porous and
, porous and 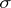 -porous sets take the role of sets of measure zero. If
-porous sets take the role of sets of measure zero. If 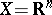 and
and 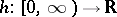 is an increasing continuous function with
is an increasing continuous function with 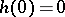 , then
, then 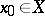 is called an
is called an 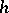 -porous point of a set
-porous point of a set  if
if 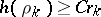 , using the same notations (
, using the same notations (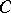 is independent of
is independent of 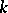 ). The concepts of
). The concepts of 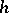 -porous and
-porous and 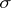 -
-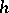 -porous sets are defined accordingly. In the case
-porous sets are defined accordingly. In the case 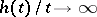 (
(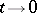 ), a
), a 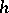 -porous set
-porous set 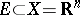 may be a set of positive Lebesgue measure.
may be a set of positive Lebesgue measure.
References
| [1] | E.P. Dolzhenko, "Boundary properties of arbitrary functions" Math. USSR Izv. , 1 : 1 (1967) pp. 1–12 Izv. Akad. Nauk. SSSR Ser. Mat. , 31 : 1 (1967) pp. 3–14 |
| [2] | L. Zajiček, "Sets of 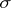 -porosity and sets of -porosity and sets of 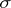 -porosity -porosity 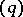 " Casopis. Pešt. Mat. , 101 (1976) pp. 350–359 " Casopis. Pešt. Mat. , 101 (1976) pp. 350–359 |
| [3] | J. Foran, P.D. Humke, "Some set-theoretic properties of 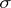 -porous sets" Real Anal. Exch. , 6 : 1 (1980/81) pp. 114–119 -porous sets" Real Anal. Exch. , 6 : 1 (1980/81) pp. 114–119 |
| [4] | J. Tkadlec, "Constructions of some non-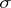 - -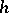 -porous sets on the real line" Real Anal. Exch. , 9 : 2 (1983/84) pp. 473–482 -porous sets on the real line" Real Anal. Exch. , 9 : 2 (1983/84) pp. 473–482 |
| [5] | S.J. Agronsky, A.M. Bruckner, "Local compactness and porosity in metric spaces" Real Anal. Exch. , 11 : 2 (1985/86) pp. 365–379 |
| [6] | Yu.A. Shevchenko, "On Vitali's covering theorem" Vestnik Moskov. Univ. Ser. 1. Mat. Mech. : 3 (1989) pp. 11–14 (In Russian) |
Porosity point. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Porosity_point&oldid=48246