Plessner theorem
One of the basic results in the theory of boundary properties of analytic functions. Let 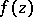 be a meromorphic function in the unit disc
be a meromorphic function in the unit disc 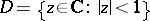 and let
and let 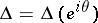 be the open angle with vertex
be the open angle with vertex 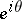 on the circle
on the circle 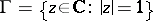 formed by two chords of
formed by two chords of  passing through
passing through 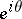 . The point
. The point 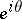 is called a Plessner point (or it is said that
is called a Plessner point (or it is said that 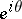 has the Plessner property) if in every arbitrarily small angle
has the Plessner property) if in every arbitrarily small angle  there exists a sequence
there exists a sequence 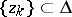 such that
such that
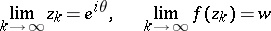 |
for every value 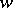 in the extended complex plane
in the extended complex plane 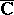 . The point
. The point 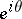 is called a Fatou point for
is called a Fatou point for 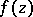 if there exists a single unique limit
if there exists a single unique limit
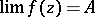 |
as  tends to
tends to 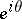 within any angle
within any angle 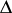 . Plessner's theorem [1]: Almost-all points on
. Plessner's theorem [1]: Almost-all points on 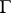 with respect to the Lebesgue measure on
with respect to the Lebesgue measure on 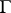 are either Fatou points or Plessner points.
are either Fatou points or Plessner points.
It is also known that the set 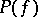 of all Plessner points has type
of all Plessner points has type 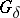 on
on 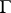 . Examples have been constructed of analytic functions in
. Examples have been constructed of analytic functions in  for which
for which  is dense on
is dense on  and has arbitrary given Lebesgue measure
and has arbitrary given Lebesgue measure  ,
, 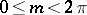 [3]. Plessner's theorem applies to any meromorphic function
[3]. Plessner's theorem applies to any meromorphic function 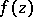 in any simply-connected domain
in any simply-connected domain 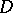 with a rectifiable boundary
with a rectifiable boundary 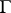 . In that case,
. In that case, 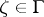 is a Fatou point if the following limit exists (cf. also Cluster set):
is a Fatou point if the following limit exists (cf. also Cluster set):
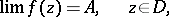 |
as 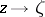 along any non-tangential path; the definition of a Plessner point
along any non-tangential path; the definition of a Plessner point 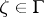 must be altered in such a way that one considers angles
must be altered in such a way that one considers angles 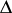 with vertex
with vertex  and sides forming angles less than
and sides forming angles less than 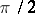 with the normal to
with the normal to 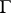 at
at  [2].
[2].
Meier's theorem is an analogue of Plessner's theorem in terms of categories of sets (cf. Meier theorem).
References
| [1] | A.I. Plessner, "Über das Verhalten analytischer Funktionen auf dem Rande des Definitionsbereiches" J. Reine Angew. Math. , 158 (1928) pp. 219–227 |
| [2] | I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
| [3] | A.J. Lohwater, "The boundary behaviour of analytic functions" Itogi Nauk. i Tekhn. Mat. Anal. , 10 (1973) pp. 99–259 (In Russian) |
Comments
Angles of the form 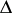 are called Stolz angles.
are called Stolz angles.
A good reference is [a3], to which [3] is a Russian sequel.
Plessner's theorem has a complete analogue for the unit ball in 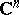 , cf. [a1]: Every holomorphic function on the unit ball decomposes the boundary into three measurable sets, as in the classical case.
, cf. [a1]: Every holomorphic function on the unit ball decomposes the boundary into three measurable sets, as in the classical case.
References
| [a1] | W. Rudin, "Function theory in the unit ball in 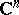 " , Springer (1981) " , Springer (1981) |
| [a2] | M. Tsuji, "Potential theory in modern function theory" , Chelsea, reprint (1975) |
| [a3] | E.F. Collingwood, A.J. Lohwater, "The theory of cluster sets" , Cambridge Univ. Press (1966) pp. Chapt. 9 |
| [a4] | K. Noshiro, "Cluster sets" , Springer (1960) |
Plessner theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Plessner_theorem&oldid=48190