Plancherel theorem

For any square-summable function 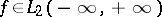the integral

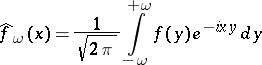converges in 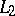to some function 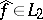as , i.e.

(1)

Here the function 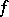itself is representable as the limit in 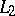of the integrals

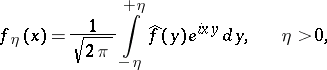as 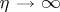, i.e.

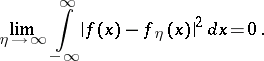Also, the following relation holds:

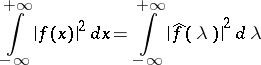(the Parseval–Plancherel formula).

The function

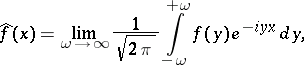where the limit is understood in the sense of convergence in 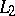(as in (1)), is called the Fourier transform of 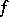; it is sometimes denoted by the symbolic formula:

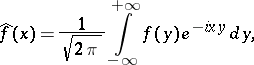(2)

where the integral in (2) must be understood in the sense of the principal value at 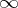in the metric of . One similarly interprets the equation

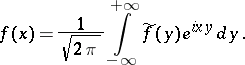(3)

For functions 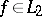, the integrals (2) and (3) exist in the sense of the principal value for almost all .

The functions 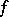and 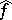also satisfy the following equations for almost-all :

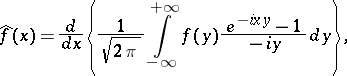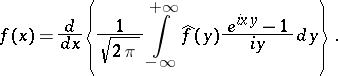If Fourier transformation is denoted by and if 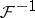denotes the inverse, then Plancherel's theorem can be rephrased as follows: 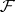and 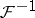are mutually-inverse unitary operators on 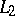(cf. Unitary operator).

The theorem was established by M. Plancherel (1910).

References

[1]	A. Zygmund, "Trigonometric series" , 2 , Cambridge Univ. Press (1988)
[2]	E.C. Titchmarsh, "Introduction to the theory of Fourier integrals" , Oxford Univ. Press (1948)
[3]	S. Bochner, "Lectures on Fourier integrals" , Princeton Univ. Press (1959) (Translated from German)

Comments

The heart of Plancherel's theorem is the assertion that if 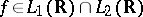, then: a) 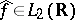, where 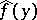is defined by (2) for 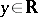; b) 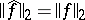; and c) the set of all such 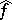is dense in 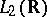. Then one extends this mapping 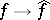to a unitary mapping 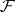of 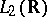onto itself which satisfies 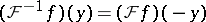for almost every 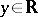. There are generalizations of Plancherel's theorem in which 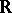is replaced by 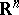or by any locally compact Abelian group. Cf. also Harmonic analysis, abstract.

References

[a1]	W. Rudin, "Fourier analysis on groups" , Wiley (1962)
[a2]	A. Weil, "l'Intégration dans les groupes topologiques et ses applications" , Hermann (1940)
[a3]	L.S. Pontryagin, "Topological groups" , Princeton Univ. Press (1958) (Translated from Russian)
[a4]	E. Hewitt, K.A. Ross, "Abstract harmonic analysis" , 1–2 , Springer (1979)
[a5]	H. Reiter, "Classical harmonic analysis and locally compact groups" , Oxford Univ. Press (1968)