Place of a field
with values in a field 
, 
-valued place of a field 
A mapping 
satisfying the conditions
 |
 |
 |
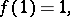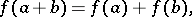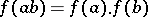(provided that the expressions on the right-hand sides are defined). The following conventions are made:
 |
 |
 |
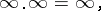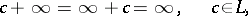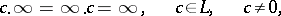while the expressions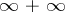 
, 
and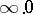 
are undefined.
An element 
in 
for which 
is called finite in the place 
; the set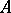 
of finite elements is a subring of 
, and the mapping 
is a ring homomorphism. The ring 
is a local ring, its maximal ideal is 
.
A place 
determines a valuation 
of 
with group of values 
(where 
and 
are, respectively, the groups of invertible elements of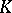 
and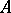 
). The ring of this valuation is the same as 
. Conversely, any valuation 
of a field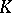 
determines a place of 
with values in the residue class field of 
. Here, the ring of finite elements is the same as the ring of (integers of) the valuation 
.
References
| [1] | S. Lang, "Algebra" , Addison-Wesley (1984) |
Comments
References
| [a1] | P.M. Cohn, "Algebra" , 2 , Wiley (1977) pp. Chapt. 9 |
Place of a field. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Place_of_a_field&oldid=48183