Permutation test
A statistical test intended for testing the hypothesis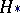 
according to which the probability density (cf. Density of a probability distribution) of an observable random vector 
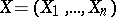belongs to the family of all 
-dimensional densities that are symmetric with respect to permutation of their arguments.
Assume that one has to test the hypothesis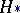 
that the probability density 
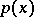of the random vector 
belongs to the family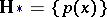 
of all 
-dimensional densities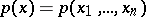 
that are symmetric with respect to permutation of the arguments 
, from a realization of the random vector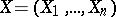 
that takes values 
in 
-dimensional Euclidean space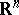 
. Then
 |
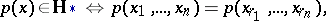where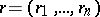 
is any vector from the space 
of all permutations 
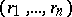of the vector 
. The space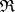 
is the set of all realizations of the vector of ranks 
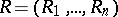naturally arising in constructing the order statistic vector 
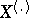that takes values 
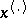in the set 
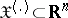. If 
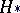is true, then the statistics 
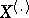and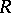 
are stochastically independent, and
 | (*) |
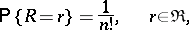and the probability density for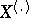 
is 
, 
.
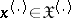Property (*) of the uniform distribution for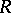 
if 
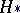is true forms the basis of constructing the permutation test.
If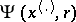 
is a function defined on 
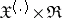in such a way that 
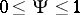and such that for any 
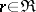it is measurable with respect to the Borel 
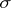-algebra of 
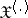, and if also for some 
,
 |
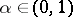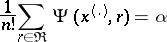almost-everywhere, then the statistical test for testing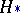 
with critical function
 |
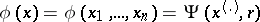is called the permutation test. If the permutation test is not randomized,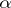 
should be taken a multiple of 
.
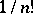The most-powerful test for testing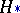 
against a simple alternative 
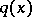can be found in the family of permutation tests, where 
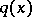is any 
-dimensional density not belonging to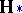 
.
The family of permutation tests and the family of tests that are invariant under a change in the shift and scale parameters play significant roles in constructing rank tests (cf. Rank test). Finally, in the literature on mathematical statistics, one frequently finds the term permutation test replaced by "randomization test" .
See Order statistic; Invariant test; Critical function.
References
| [1] | J. Hájek, Z. Sidák, "Theory of rank tests" , Acad. Press (1967) |
| [2] | E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1986) |
Permutation test. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Permutation_test&oldid=48162