Perfect compactification
A compactification 
of a completely-regular space 
such that the closure in 
of the boundary of any open set 
coincides with the boundary of 
, where 
is the maximal open set in 
for which 
. Equivalent definitions are as follows:
a) 
for any pair of disjoint open sets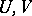 
;
b) if a closed set 
partitions 
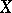into open sets 
and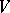 
, then the closure of 
in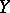 
partitions 
into 
and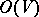 
;
c) 
does not partition 
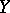locally at any of its points.
A compactification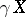 
is perfect if and only if the natural mapping 
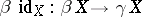is monotone; here 
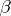is the Stone–Čech compactification of 
. Also,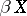 
is the unique perfect compactification of 
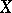if and only if 
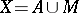with 
a compactum and 
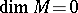. The local connectedness of 
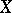implies the local connectedness of any perfect extension 
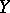of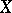 
satisfying the first axiom of countability (and also the local connectedness of all intermediate extensions). Among all the perfect compactifications of 
there is a minimal one, 
, if and only if 
has at least one compactification with punctiform remainder (cf. Remainder of a space). The remainder in 
is punctiform and 
is the maximal such extension among those with punctiform remainder. Every homeomorphism of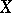 
extends to a homeomorphism of 
, and every perfect mapping from 
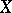onto 
extends to a mapping from 
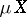onto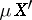 
(provided 
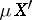exists).
Comments
A space is called punctiform if and only if no compact connected subset contains more than one point.
References
| [a1] | A.V. Arkhangel'skii, V.I. Ponomarev, "Fundamentals of general topology: problems and exercises" , Reidel (1984) pp. 232ff (Translated from Russian) |
Perfect compactification. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Perfect_compactification&oldid=48153