Pendulum equation

An ordinary differential equation of the form

(*)

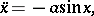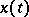where is a positive constant. A pendulum equation arises in the study of free oscillations of a mathematical pendulum in a gravity field — a point mass with one degree of freedom attached to the end of a non-extendible and incompressible weightless suspender, the other end of which is fastened on a hinge which permits the pendulum to rotate in a vertical plane. The unknown function is the deviation angle of the pendulum at time 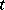from the lower equilibrium position, measured in radians;

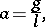where is the length of the suspender and 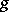is the gravitational acceleration. The (approximate) equation describing the small oscillations of the pendulum about the lower equilibrium position has the form

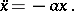The qualitative investigation of the pendulum equation is carried out using the law of conservation of energy, which relates the position and the velocity of the pendulum:

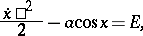where 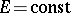is the total energy of the pendulum. The time scale can be chosen so that 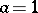. Then for an energy value 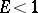the pendulum performs an oscillatory movement (the velocity changes its sign periodically), whereas for 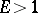it rotates (the velocity has constant sign). The solution 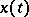of (*) with initial condition 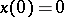, 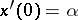for 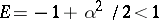, satisfies the relation

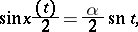where the Jacobi elliptic function 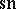has modulus 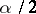(cf. Jacobi elliptic functions).

Of great practical importance are equations close to the pendulum equation. The presence of a small friction that depends on the position and velocity of the pendulum leads to the equation

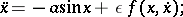the small oscillations of the pendulum with friction are described by the equation

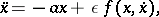a particular case of which is the van der Pol equation. The oscillations of a pendulum for which the length of the suspender varies periodically (the motion of a swing) are described by the Hill equation, an important particular case of which is the Mathieu equation.

References

[1]	V.I. Arnol'd, "Ordinary differential equations" , M.I.T. (1973) (Translated from Russian)
[2]	E. Kamke, "Differentialgleichungen: Lösungen und Lösungsmethoden" , 1. Gewöhnliche Differentialgleichungen , Chelsea, reprint (1971)
[3]	A.A. Andronov, A.A. Vitt, A.E. Khaikin, "Theory of oscillators" , Dover, reprint (1987) (Translated from Russian)

Comments

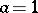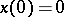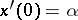For and , with 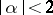the motion is periodic with amplitude

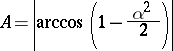and period

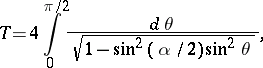which is a complete elliptic integral of the first kind, see [a1]. The periodically-forced damped pendulum

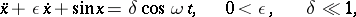and the parametrically-forced damped pendulum

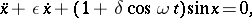give rise to chaotic solutions. These are analyzed with Melnikov's method in, respectively, [a1] and [a3]. In [a4] the class of problems

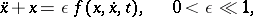is studied with perturbation methods (cf. also Perturbation theory). Special attention is given to the averaging method (cf. e.g. Krylov–Bogolyubov method of averaging).

References

[a1]	J.K. Hale, "Ordinary differential equations" , Wiley (Interscience) (1969)
[a2]	J. Guckenheimer, P. Holmes, "Nonlinear oscillations, dynamical systems, and bifurcation of vectorfields" , Springer (1983)
[a3]	S. Wiggins, "Global bifurcations and chaos" , Springer (1988)
[a4]	J.A. Sanders, F. Verhulst, "Averaging methods in nonlinear dynamical systems" , Springer (1985)
[a5]	V.I. Arnol'd, A. Avez, "Problèmes ergodiques de la mécanique classique" , Gauthier-Villars (1967) (Translated from Russian)