Path
A continuous mapping 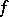 of the interval
of the interval 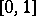 into a topological space
into a topological space 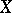 . The points
. The points 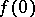 and
and 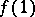 are called the initial and the final points of the path
are called the initial and the final points of the path 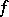 . Given
. Given 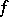 , the path defined by the formula
, the path defined by the formula 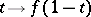 ,
, 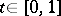 , is called the path inverse to
, is called the path inverse to 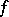 and is denoted by
and is denoted by 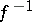 . Given
. Given 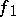 and
and 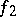 with
with 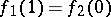 , the path defined by the formula
, the path defined by the formula
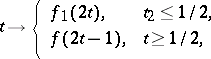 |
is called the composite of the paths 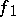 and
and 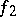 and is denoted by
and is denoted by 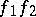 . In a path-connected space
. In a path-connected space 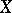 with distinguished point
with distinguished point  , the set of all paths with initial point
, the set of all paths with initial point  forms the path space of
forms the path space of 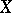 .
.
Comments
Generally one is interested not so much in the individual paths in a space as in the homotopy classes thereof; if one factors by the equivalence relation of homotopy relative to 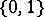 , the composition defined above becomes associative, and
, the composition defined above becomes associative, and 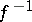 becomes a genuine inverse to
becomes a genuine inverse to 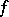 . See Fundamental groupoid.
. See Fundamental groupoid.
More precisely, one may define a path as being any continuous mapping 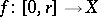 , where
, where 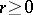 is called the length of the path
is called the length of the path 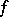 . Then
. Then 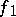 and
and 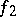 , with
, with 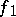 of length
of length  and
and 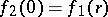 , are composed to
, are composed to 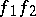 , taking
, taking 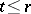 to
to 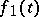 and
and  in
in 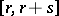 (where
(where 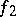 has length
has length  ) to
) to 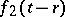 . This composition is associative (not only homotopy associative).
. This composition is associative (not only homotopy associative).
References
| [a1] | P.J. Hilton, S. Wylie, "Homology theory. An introduction to algebraic topology" , Cambridge Univ. Press (1965) |
Path. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Path&oldid=48142