Orthogonal array
orthogonal table, 
A  -dimensional matrix whose entries are the numbers
-dimensional matrix whose entries are the numbers 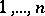 , and possessing the property that in each of its
, and possessing the property that in each of its 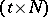 -dimensional submatrices any of the
-dimensional submatrices any of the  possible
possible  -dimensional vector-columns with these numbers as coordinates is found in the columns of this submatrix precisely
-dimensional vector-columns with these numbers as coordinates is found in the columns of this submatrix precisely 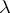 times. The definition of an orthogonal array implies that
times. The definition of an orthogonal array implies that  . One often considers the special case
. One often considers the special case  with
with 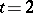 and
and 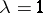 , which is then denoted by
, which is then denoted by 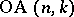 . When
. When 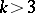 , an orthogonal array
, an orthogonal array 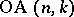 is equivalent to a set of
is equivalent to a set of 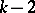 pairwise orthogonal Latin squares. For given
pairwise orthogonal Latin squares. For given 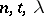 , the maximum value of the parameter
, the maximum value of the parameter 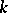 has been determined only in a number of specific cases, such as, for example,
has been determined only in a number of specific cases, such as, for example, 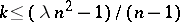 when
when 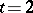 , or
, or 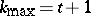 when
when 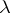 is odd and
is odd and 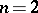 .
.
References
| [1] | J. Dénes, A.D. Keedwell, "Latin squares and their applications" , Acad. Press (1974) |
| [2] | M. Hall, "Combinatorial theory" , Wiley (1986) |
Comments
Regarding existence, the only general result for 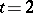 and
and  states the existence of
states the existence of 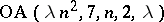 for all
for all  (H. Hanani, cf. [a1]). For
(H. Hanani, cf. [a1]). For 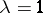 , see Orthogonal Latin squares. In geometric terms, an
, see Orthogonal Latin squares. In geometric terms, an 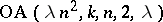 is equivalent to a "transversal designtransversal design" , respectively a "netnet" ; cf. [a1] for some fundamental results and [a2] for a recent survey.
is equivalent to a "transversal designtransversal design" , respectively a "netnet" ; cf. [a1] for some fundamental results and [a2] for a recent survey.
References
| [a1] | T. Beth, D. Jungnickel, H. Lenz, "Design theory" , Cambridge Univ. Press (1986) |
| [a2] | D. Jungnickel, "Latin squares, their geometries and their groups. A survey" , Proc. IMA Workshops on Coding and Design Theory Minneapolis, 1988 , Springer (to appear) |
Orthogonal array. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Orthogonal_array&oldid=48073