Normally-solvable operator
A linear operator with closed range. Let 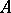 be a linear operator with dense domain in a Banach space
be a linear operator with dense domain in a Banach space 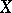 and with range
and with range 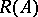 in a Banach space
in a Banach space 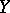 . Then
. Then  is normally solvable if
is normally solvable if 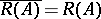 , that is, if
, that is, if 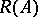 is a closed subspace of
is a closed subspace of 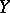 . Let
. Let 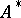 be the adjoint of
be the adjoint of 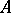 . For
. For 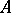 to be normally solvable it is necessary and sufficient that
to be normally solvable it is necessary and sufficient that 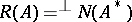 , that is, that the range of
, that is, that the range of 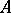 is the orthogonal complement to the null space of
is the orthogonal complement to the null space of 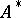 .
.
Suppose that
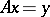 | (*) |
is an equation with a normally-solvable operator (a normally-solvable equation). If 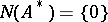 , that is, if the homogeneous adjoint equation
, that is, if the homogeneous adjoint equation 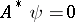 has only the trivial solution, then
has only the trivial solution, then 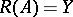 . But if
. But if 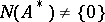 , then for (*) to be solvable it is necessary and sufficient that
, then for (*) to be solvable it is necessary and sufficient that 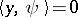 for all solutions of the equation
for all solutions of the equation 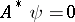 .
.
From now on suppose that  is closed. A normally-solvable operator is called
is closed. A normally-solvable operator is called  -normal if its null space
-normal if its null space 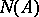 is finite dimensional
is finite dimensional 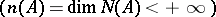 . A normally-solvable operator
. A normally-solvable operator  is called
is called 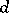 -normal if its deficiency subspace is finite dimensional
-normal if its deficiency subspace is finite dimensional 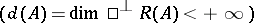 . Operators that are either
. Operators that are either  -normal or
-normal or 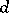 -normal are sometimes called semi-Fredholm operators. For an operator
-normal are sometimes called semi-Fredholm operators. For an operator 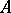 to be
to be  -normal it is necessary and sufficient that the pre-image of every compact set in
-normal it is necessary and sufficient that the pre-image of every compact set in 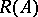 is locally compact.
is locally compact.
Suppose that  is compactly imbedded in a Banach space
is compactly imbedded in a Banach space 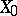 . For
. For 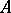 to be
to be  -normal it is necessary and sufficient that there is an a priori estimate
-normal it is necessary and sufficient that there is an a priori estimate
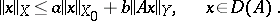 |
It turns out that an operator  is
is  -normal if and only if
-normal if and only if 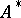 is
is 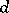 -normal. Then
-normal. Then 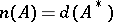 . Consequently, if
. Consequently, if 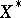 is compactly imbedded in a Banach space
is compactly imbedded in a Banach space 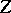 , then
, then 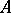 is
is 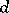 -normal if and only if there is an a priori estimate
-normal if and only if there is an a priori estimate
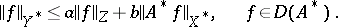 |
The pair of numbers 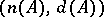 is called the
is called the 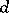 -characteristic of
-characteristic of  . If a normally-solvable operator
. If a normally-solvable operator 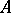 is
is  -normal or
-normal or 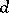 -normal, the number
-normal, the number
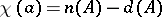 |
is called the index of the operator  . The properties of being
. The properties of being  -normal and
-normal and 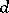 -normal are stable: If
-normal are stable: If  is
is  -normal (or
-normal (or 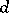 -normal) and
-normal) and 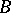 is a linear operator of small norm or completely continuous, then
is a linear operator of small norm or completely continuous, then 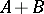 is also
is also  -normal (respectively,
-normal (respectively, 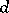 -normal).
-normal).
References
| [1] | F. Hausdorff, "Grundzüge der Mengenlehre" , Leipzig (1914) (Reprinted (incomplete) English translation: Set theory, Chelsea (1978)) |
| [2] | F. Atkinson, "Normal solvability of equations in Banach space" Mat. Sb. , 28 : 1 (1951) pp. 3–14 (In Russian) |
| [3] | S.G. Krein, "Linear differential equations in Banach space" , Transl. Math. Monogr. , 29 , Amer. Math. Soc. (1971) (Translated from Russian) |
Comments
References
| [a1] | I.C. [I.Ts. Gokhberg] Gohberg, M.G. Krein, "The basic propositions on defect numbers, root numbers and indices of linear operators" Transl. Amer. Math. Soc. (2) , 13 (1960) pp. 185–264 Uspekhi Mat. Nauk , 12 (1957) pp. 43–118 |
| [a2] | S. Goldberg, "Unbounded linear operators" , McGraw-Hill (1966) |
| [a3] | T. Kato, "Perturbation theory for nullity, deficiency and other quantities of linear operators" J. d'Anal. Math. , 6 (1958) pp. 261–322 |
| [a4] | S.G. Krein, "Linear equations in Banach spaces" , Birkhäuser (1982) (Translated from Russian) |
Normally-solvable operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Normally-solvable_operator&oldid=48021