Normal operator
A closed linear operator  defined on a linear subspace
defined on a linear subspace  that is dense in a Hilbert space
that is dense in a Hilbert space  such that
such that  , where
, where  is the operator adjoint to
is the operator adjoint to  . If
. If  is normal, then
is normal, then  and
and  for every
for every  . Conversely, these conditions guarantee that
. Conversely, these conditions guarantee that 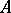 is normal. If
is normal. If 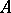 is normal, then so are
is normal, then so are  ;
;  for any
for any 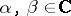 ;
; 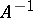 when it exists; and if
when it exists; and if  , where
, where 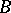 is a bounded linear operator, then also
is a bounded linear operator, then also 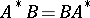 .
.
A normal operator has:
1) the multiplicative decomposition
 |
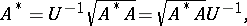 |
where 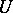 is a unitary operator which is uniquely determined on the orthogonal complement of the null space of
is a unitary operator which is uniquely determined on the orthogonal complement of the null space of 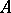 and
and 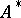 ;
;
2) the additive decomposition
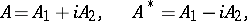 |
where 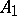 and
and 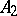 are uniquely determined self-adjoint commuting operators.
are uniquely determined self-adjoint commuting operators.
The additive decomposition implies that for an ordered pair 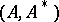 there exists a unique two-dimensional spectral function
there exists a unique two-dimensional spectral function 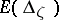 , where
, where 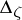 is a two-dimensional interval,
is a two-dimensional interval, 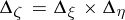 ,
, 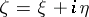 , such that
, such that
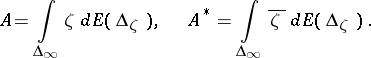 |
The same decomposition also implies that a normal operator 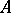 is a function of a certain self-adjoint operator
is a function of a certain self-adjoint operator 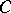 ,
, 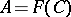 . Conversely, every function of some self-adjoint operator is normal.
. Conversely, every function of some self-adjoint operator is normal.
An important property of a normal operator 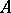 is the fact that
is the fact that 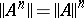 , which implies that the spectral radius of a normal operator
, which implies that the spectral radius of a normal operator 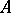 is its norm
is its norm 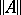 . Eigen elements of a normal operator corresponding to distinct eigen values are orthogonal.
. Eigen elements of a normal operator corresponding to distinct eigen values are orthogonal.
References
| [1] | A.I. Plesner, "Spectral theory of linear operators" , F. Ungar (1965) (Translated from Russian) |
| [2] | W. Rudin, "Functional analysis" , McGraw-Hill (1973) |
Comments
References
| [a1] | J.B. Conway, "Subnormal operators" , Pitman (1981) |
Normal operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Normal_operator&oldid=48015