Mutual kernels

reciprocal kernels

Two functions 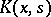and 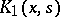of real variables 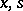(or, in general, of points 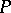and 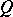of a Euclidean space), defined on the square 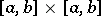and satisfying the condition

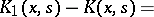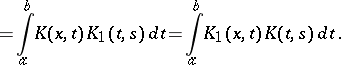If a kernel 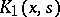reciprocal with 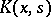exists, then is the resolvent kernel of the integral Fredholm equation

(*)

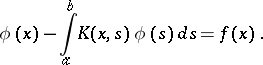Comments

Indeed, when and 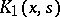are reciprocal kernels, the solution of equation (*) above is given by

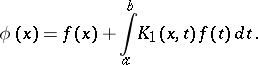Consider the Fredholm equation

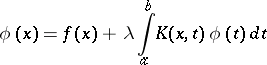(a1)

and the iterated kernels ,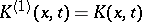

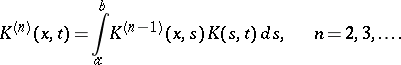Form the Neumann series

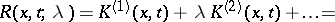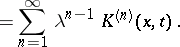If 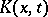is continuous on 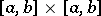, this series is uniformly convergent for 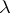small. Then 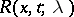satisfies

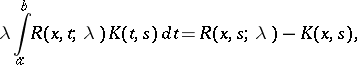and

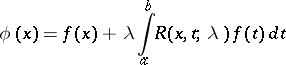solves (a1).

The terminology "mutual kernels" and "reciprocal kernels" is rarely used.

References

[a1]	V.I. Smirnov, "A course of higher mathematics" , 4 , Addison-Wesley (1964) (Translated from Russian)
[a2]	P.P. Zabreiko (ed.) A.I. Koshelev (ed.) M.A. Krasnoselskii (ed.) S.G. Mikhlin (ed.) L.S. Rakovshchik (ed.) V.Ya. Stet'senko (ed.) T.O. Shaposhnikova (ed.) R.S. Anderssen (ed.) , Integral equations - a reference text , Noordhoff (1975) (Translated from Russian)
[a3]	B.L. Moiseiwitsch, "Integral equations" , Longman (1977)