Multi-dimensional variational problem
variational problem involving partial derivatives
A problem in the calculus of variations (cf. Variational calculus) in which it is required to determine an extremum of a functional depending on a function of several independent variables. Ordinary variational problems, in which functionals of functions of one independent variable are considered, may be called one-dimensional variational problems, in this sense.
An example of a two-dimensional variational problem is the problem of determining a function of two independent variables, 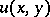 , which, together with its first-order partial derivatives, is continuous and yields an extremum of the functional
, which, together with its first-order partial derivatives, is continuous and yields an extremum of the functional
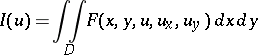 | (1) |
under the boundary condition
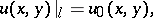 | (2) |
where 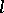 is a closed contour bounding a domain
is a closed contour bounding a domain 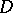 ,
, 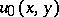 is a given function and
is a given function and 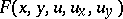 is a twice continuously-differentiable function jointly in its arguments. Let
is a twice continuously-differentiable function jointly in its arguments. Let 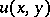 be a solution of the problem (1), (2). Substitution of a comparison function
be a solution of the problem (1), (2). Substitution of a comparison function 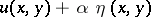 , where
, where 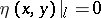 and
and 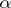 is a numerical parameter, into (1), differentiation with respect to
is a numerical parameter, into (1), differentiation with respect to 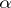 and equating
and equating 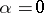 , gives the following expression for the first variation of the functional:
, gives the following expression for the first variation of the functional:
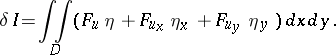 | (3) |
If 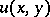 has continuous second-order derivatives, then it is easy to show that a necessary condition for
has continuous second-order derivatives, then it is easy to show that a necessary condition for 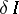 to vanish is:
to vanish is:
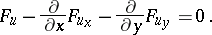 | (4) |
Equation (4) is called the Euler–Ostrogradski equation (sometimes the Ostrogradski equation). This equation must be satisfied by a function  which gives an extremum of (1) under the boundary conditions (2). The Euler–Ostrogradski equation is analogous to the Euler equation for one-dimensional problems. In expanded form, (4) is a second-order partial differential equation.
which gives an extremum of (1) under the boundary conditions (2). The Euler–Ostrogradski equation is analogous to the Euler equation for one-dimensional problems. In expanded form, (4) is a second-order partial differential equation.
In the case of a triple integral and a function  depending on three independent variables, the Euler–Ostrogradski equation takes the form:
depending on three independent variables, the Euler–Ostrogradski equation takes the form:
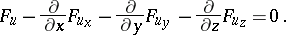 |
The following condition is an analogue of the Legendre condition. In order that 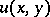 gives at least a weak extremum of (1) it is necessary that at each interior point of
gives at least a weak extremum of (1) it is necessary that at each interior point of 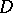 ,
,
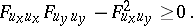 |
For a minimum necessarily 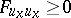 , and for a maximum
, and for a maximum 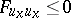 .
.
Discontinuous multi-dimensional variational problems have also been considered (see [4]).
References
| [1] | R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , 2 , Interscience (1965) (Translated from German) |
| [2] | V.I. Smirnov, "A course of higher mathematics" , 4 , Addison-Wesley (1964) (Translated from Russian) |
| [3] | N.I. Akhiezer, "The calculus of variations" , Blaisdell (1962) (Translated from Russian) |
| [4] | M.K. Kerimov, "On two-dimensional continuous problems of variational calculus" Trudy Tbilis. Mat. Inst. Akad. Nauk GruzSSR , 18 (1951) pp. 209–219 (In Russian) |
Multi-dimensional variational problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Multi-dimensional_variational_problem&oldid=47916