Monomial substitutions, group of
The subgroup of the group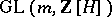 
of all invertible matrices of order 
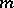over the integral group ring 
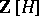(see Group algebra) of a group 
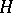, consisting of all matrices which precisely contain one non-zero element of 
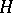in each row and column. Each such matrix, having a non-zero element 
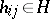in place 
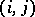, corresponds to a monomial substitution, that is, a mapping 
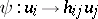, where 
, 
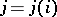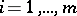, and 
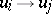is a permutation of the finite set 
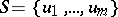. The product of such mappings is given by the formula
 |
(
, 
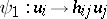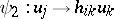), and corresponds to the product of the matrices associated with 
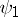and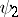 
. Any group 
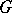containing 
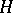as a subgroup of index 
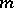can be isomorphically imbedded in a group of monomial substitutions. The group of monomial substitutions is isomorphic to the (unrestricted) wreath product of 
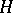with the symmetric group 
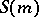of degree 
.
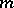References
| [1] | M.I. Kargapolov, J.I. [Yu.I. Merzlyakov] Merzljakov, "Fundamentals of the theory of groups" , Springer (1979) (Translated from Russian) |
| [3] | M. Hall jr., "The theory of groups" , Macmillan (1959) |
Monomial substitutions, group of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Monomial_substitutions,_group_of&oldid=47892