Monogeneity set
The set of all derived numbers (Dini derivatives, cf. Dini derivative) of a given function of a complex variable at a given point. More precisely, let 
be a set in the complex plane 
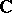, let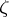 
be a non-isolated point of 
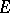and let 
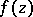be a complex function of 
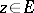. A complex number 
(proper or equal to 
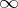) is called a derived number (or Dini derivative) of 
at 
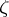relative to 
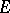if there is a sequence 
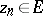with the properties: 
, 
,
 |
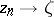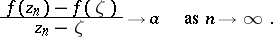The set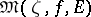 
of all derived numbers of 
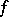at 
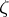relative to 
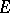is called the monogeneity set of 
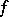at 
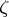relative to 
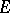(see [1]). The set 
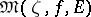consists of a unique finite point 
if and only if 
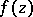is a monogenic function at 
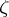relative to 
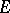and 
. The set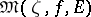 
is always closed, and for each closed set 
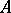in the extended complex plane 
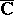, each set 
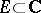and each finite non-isolated point 
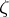of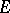 
, there is a function 
, 
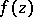, such that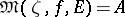 
. If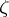 
is an interior point of 
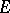, then for any function 
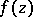that is continuous in a neighbourhood of 
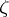, the set 
is closed and connected (a continuum) in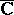 
and, conversely, for any continuum 
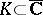there is a function 
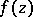, continuous in a neighbourhood of 
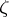, for which 
. If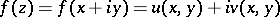 
is differentiable with respect to the set of real variables 
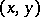at an interior point 
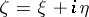of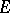 
, then 
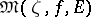is the circle 
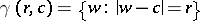(possibly degenerating into a point, 
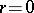) with centre 
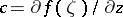and radius 
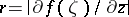, where
 |
 |
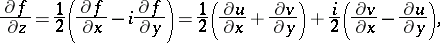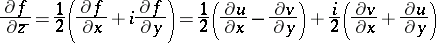are the so-called formal derivatives. The converse is also true: Each circle is the monogeneity set for some function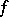 
, differentiable with respect to 
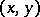, at a given interior point 
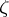of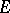 
.
If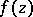 
is continuous in a domain 
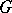, then at almost every 
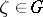the set 
is either a circle 
, 
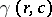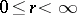, or is 
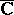(see [2]). In the general case of an arbitrary (not necessarily measurable) set 
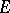and an arbitrary (not necessarily measurable) finite function 
, 
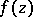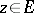, at almost every point 
one of the following three cases holds: a) 
, 
, 
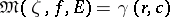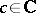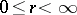; b)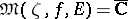 
; or c) 
, 
, 
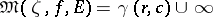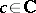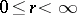. Here, a) holds at almost every differentiability point of 
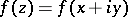with respect to 
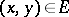and one of the first two cases holds at almost every continuity point of 
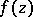. Each of the cases a)–c) may be realized individually at almost every point 
.
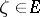For some natural generalizations to the multi-dimensional case see [4].
References
| [1] | V.S. Fedorov, "The work of N.N. Luzin on the theory of functions of a complex variable" Uspekhi Mat. Nauk , 7 : 2 (1952) pp. 7–16 (In Russian) |
| [2] | Yu.Yu. Trokhimchuk, "Continuous mappings and monogeneity conditions" , Moscow (1963) (In Russian) |
| [3] | E.P. Dolzhenko, "On the derived numbers of complex functions" Izv. Akad. Nauk SSSR Ser. Mat. , 26 (1962) pp. 347–360 (In Russian) |
| [4] | A.V. Bondar, "Continuous operator conformal mappings" Ukr. Math. J. , 32 : 3 (1980) pp. 207–212 Ukrain. Mat. Zh. , 32 : 3 (1980) pp. 314–322 |
Monogeneity set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Monogeneity_set&oldid=47886