Moduli of a Riemann surface
Numerical characteristics (parameters) which are one and the same for all conformally-equivalent Riemann surfaces, and in their totality characterize the conformal equivalence class of a given Riemann surface. Here two Riemann surfaces  and
and  are called conformally equivalent if there is a conformal mapping from
are called conformally equivalent if there is a conformal mapping from  onto
onto  . For example, the conformal classes of compact Riemann surfaces of topological genus
. For example, the conformal classes of compact Riemann surfaces of topological genus  are characterized by
are characterized by  real moduli; a Riemann surface of torus type
real moduli; a Riemann surface of torus type  is characterized by 2 moduli; an
is characterized by 2 moduli; an  -connected plane domain, considered as a Riemann surface with boundary, is characterized by
-connected plane domain, considered as a Riemann surface with boundary, is characterized by  moduli for
moduli for 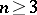 . About the structure of the moduli space of a Riemann surface see Riemann surfaces, conformal classes of.
. About the structure of the moduli space of a Riemann surface see Riemann surfaces, conformal classes of.
A necessary condition for the conformal equivalence of two plane domains is that they have the same connectivity. According to the Riemann theorem, all simply-connected domains with more than one boundary point are conformally equivalent to each other; each such domain can be conformally mapped onto one canonical domain, usually taken to be the unit disc. For  -connected domains,
-connected domains, 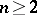 , a precise equivalent of this Riemann mapping theorem does not exist: It is impossible to give any fixed domain whatever onto which it is possible to univalently and conformally map all domains of a given order of connectivity. This has led to a more flexible definition of a canonical
, a precise equivalent of this Riemann mapping theorem does not exist: It is impossible to give any fixed domain whatever onto which it is possible to univalently and conformally map all domains of a given order of connectivity. This has led to a more flexible definition of a canonical  -connected domain, which reflects the general geometric structure of this domain, but does not fix its moduli (see Conformal mapping).
-connected domain, which reflects the general geometric structure of this domain, but does not fix its moduli (see Conformal mapping).
Each doubly-connected domain 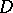 of the
of the  -plane with non-degenerate boundary continua can be conformally mapped onto some circular annulus
-plane with non-degenerate boundary continua can be conformally mapped onto some circular annulus 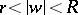 ,
, 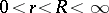 . The ratio
. The ratio 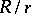 of the radii of the boundary circles of this annulus is a conformal invariant and is called the modulus of the doubly-connected domain
of the radii of the boundary circles of this annulus is a conformal invariant and is called the modulus of the doubly-connected domain 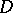 . Let
. Let 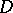 be an
be an  -connected domain,
-connected domain, 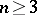 , with a non-degenerate boundary.
, with a non-degenerate boundary. 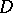 can be conformally mapped onto some
can be conformally mapped onto some  -connected circular domain
-connected circular domain 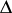 , which is a circular annulus
, which is a circular annulus 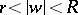 with
with 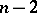 discs with bounding circles
discs with bounding circles 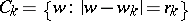 ,
, 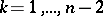 , removed; the circles
, removed; the circles 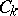 ,
, 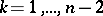 , lie in the annulus
, lie in the annulus 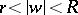 and pairwise do not have points in common. Here it can be assumed that
and pairwise do not have points in common. Here it can be assumed that 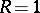 and
and  . Then
. Then 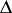 depends on
depends on 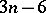 real parameters: the
real parameters: the 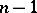 numbers
numbers 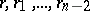 and the
and the 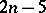 real parameters defining the centres
real parameters defining the centres  of the circles
of the circles 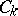 ,
,  . These
. These  real parameters can be taken as moduli of the
real parameters can be taken as moduli of the  -connected domain
-connected domain 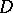 in the case
in the case 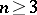 .
.
As moduli of  -connected domains
-connected domains 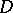 it is also possible to take any other
it is also possible to take any other 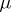 real parameters (
real parameters (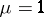 if
if 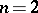 , and
, and 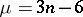 if
if 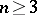 ) which determine a conformal mapping of
) which determine a conformal mapping of  onto some canonical
onto some canonical  -connected domain of another shape.
-connected domain of another shape.
References
| [1] | G. Springer, "Introduction to Riemann surfaces" , Addison-Wesley (1957) pp. Chapt. 10 |
| [2] | L. Bers, "Uniformization, moduli, and Kleinian groups" Bull. London Math. Soc. , 4 (1972) pp. 257–300 |
| [3] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
| [4] | R. Courant, "Dirichlet's principle, conformal mapping, and minimal surfaces" , Interscience (1950) (With appendix by M. Schiffer: Some recent developments in the theory of conformal mapping) |
Moduli of a Riemann surface. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Moduli_of_a_Riemann_surface&oldid=47875