Mixed autoregressive moving-average process

autoregressive moving-average process, ARMA process

A wide-sense stationary stochastic process 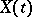with discrete time 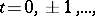the values of which satisfy a difference equation

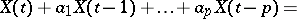(1)

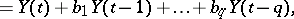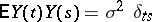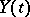where , , being the Kronecker delta (i.e. is a white noise process with spectral density 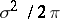), 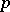and 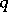are non-negative integers, and 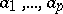, 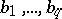are constant coefficients. If all roots of the equation

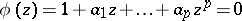are of modulus distinct from 1, then the stationary autoregressive moving-average process 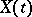exists and has spectral density

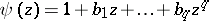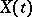where . However, for the solution of equation (1) with given initial values to tend to the stationary process as 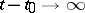, it is necessary that all roots of the equation be situated outside the unit disc 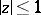(see [1] and [2], for example).

The class of Gaussian autoregressive moving-average processes coincides with the class of stationary processes that have a spectral density and are one-dimensional components of multi-dimensional Markov processes (see [3]). Special cases of autoregressive moving-average processes are auto-regressive processes (when 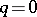, cf. Auto-regressive process) and moving-average processes (when 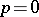, cf. Moving-average process).

Generalizations of autoregressive moving-average processes are the autoregressive integrated moving-average processes introduced by G.E.P. Box and G.M. Jenkins (see [1]) and often used in applied problems. These are non-stationary processes with stationary increments such that the increments of some fixed order form an autoregressive moving-average process.

References

[1]	G.E.P. Box, G.M. Jenkins, "Time series analysis. Forecasting and control" , 1–2 , Holden-Day (1976)
[2]	T.W. Anderson, "The statistical analysis of time series" , Wiley (1971)
[3]	J.L. Doob, "The elementary Gaussian processes" Ann. Math. Stat. , 15 (1944) pp. 229–282

Comments

The class of autoregressive moving-average processes is of interest because they represent stationary processes with a rational spectral density.

The problem of representing a stationary process as an autoregressive moving-average process is known in the Western literature as the stochastic realization problem; see [a2], [a4] for references on this problem.

Autoregressive moving-average processes are used by statisticians [a3], econometricians [a1] and engineers [a5].

References

[a1]	M. Aoki, "Notes on economic time series analysis: system theory perspectives" , Lect. notes in econom. and math. systems , 220 , Springer (1983)
[a2]	P. Faurre, M. Clerget, F. Germain, "Opérateurs rationnels positifs" , Dunod (1979)
[a3]	E.J. Hannan, "Multiple time series" , Wiley (1970)
[a4]	A. Lindquist, G. Picci, "Realization theory for multivariate stationary Gaussian processes" SIAM J. Control Optim. , 23 (1985) pp. 809–857
[a5]	L. Ljung, T. Söderström, "Theory and practice of recursive identification" , M.I.T. (1983)