Minor of a graph
Let 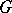 be a graph (possibly with loops and multiple edges). A minor of
be a graph (possibly with loops and multiple edges). A minor of 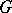 is any graph obtained by a succession of the following operations:
is any graph obtained by a succession of the following operations:
i) deletion of a single edge;
ii) contraction of a single edge;
iii) removal of an isolated vertex.
The graph minor theorem of N. Robertson and P.D. Seymour says the following. Given an infinite sequence 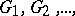 of finite graphs, there are indices
of finite graphs, there are indices 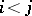 such that
such that 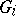 is (isomorphic to) a minor of
is (isomorphic to) a minor of 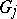 . This was conjectured by K. Wagner (Wagner's well-quasi-ordering conjecture).
. This was conjectured by K. Wagner (Wagner's well-quasi-ordering conjecture).
Let 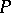 be any property of a graph which is closed under taking minors. For instance, the property of being imbeddable in a compact Riemann surface. Let
be any property of a graph which is closed under taking minors. For instance, the property of being imbeddable in a compact Riemann surface. Let 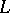 be the set of all minor-minimal isomorphism classes of graphs not possessing property
be the set of all minor-minimal isomorphism classes of graphs not possessing property 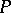 . Then the graph minor theorem says that
. Then the graph minor theorem says that 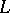 is finite. This implies that property
is finite. This implies that property  is characterized by saying that a graph has property
is characterized by saying that a graph has property 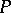 if and only if it does not contain a minor from the finite set
if and only if it does not contain a minor from the finite set 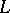 . In the case of the property "planar" the set
. In the case of the property "planar" the set 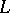 is given by the two graphs
is given by the two graphs 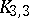 and
and 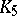 , cf. Kuratowski graph.
, cf. Kuratowski graph.
The finite forms of the graph minor theorem are as follows:
a) For all 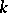 there is an
there is an  such that for
such that for  -tuples of graphs
-tuples of graphs 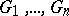 with
with 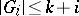 there is a pair
there is a pair 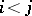 with
with 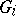 isomorphic to a minor of
isomorphic to a minor of 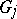 . Here
. Here 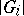 denotes the sum of the number of vertices and the number of edges of
denotes the sum of the number of vertices and the number of edges of 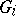 .
.
b) For all 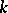 there is an
there is an  such that for all
such that for all  -tuples of graphs
-tuples of graphs 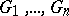 with
with 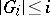 there are
there are 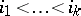 such that
such that 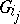 is isomorphic to a minor of
is isomorphic to a minor of 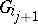 for all
for all 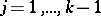 .
.
Wagner's conjecture does not hold, in general, for infinite graphs, in the sense that there is a sequence of infinite graphs 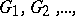 such that for all
such that for all 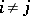 ,
, 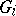 is not a minor of
is not a minor of 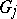 . The conjecture is open (1988) for countable graphs.
. The conjecture is open (1988) for countable graphs.
A consequence (application) is that each graph property that is closed under taking minors can be tested in polynomial time. So, for instance, planarity can be tested in polynomial time. Further, there exists a polynomial-time algorithm for the following problem: Given a graph 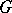 and vertices
and vertices  of
of 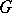 , find paths
, find paths 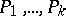 so that
so that 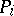 connects
connects 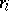 and
and 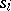 for all
for all 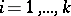 and such that the
and such that the 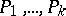 are vertex disjoint. Such problems arise in VLSI design.
are vertex disjoint. Such problems arise in VLSI design.
References
| [a1] | H. Friedman, N. Robertson, P.D. Seymour, "The metamathematics of the graph minor theorem" Logic and combinatorics (ed. S.G. Simpson) Contemporary Math. 65, Amer. Math. Soc. (1987) pp. 229–261 Zbl 0635.03060 |
| [a2] | N. Robertson, P.D. Seymour, "Graph minors - a survey" I. Anderson (ed.) , Surveys in Combinatorics 1985 , Cambridge Univ. Press (1985) pp. 153–171 Zbl 0568.05025 |
| [a3] | R. Thomas, "A counter-example to "Wagner's conjecture" for infinite graphs" Math. Proc. Cambridge Philos. Soc. , 103 (1988) pp. 55–57 Zbl 0647.05054 |
Minor of a graph. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Minor_of_a_graph&oldid=47855