Minimal iteration method

A method for solving linear algebraic equations 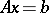, in which the solution is represented as a linear combination of basis vectors which are orthogonal in some metric connected with the matrix of the system.

In the case of a symmetric matrix , the orthogonal system of vectors 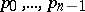is constructed using the three-term recurrence formula

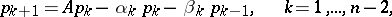(1)

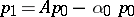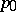, an arbitrary vector, where

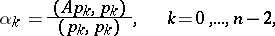The solution of the system 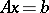is found by the formula 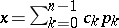, and the coefficients 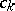are given as the solutions of the system

(2)

If the orthogonalization algorithm is degenerate, that is, if 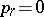for , one has to choose a new initial vector 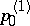, orthogonal to and one has to complete the system of basis vectors to a complete system.

In the case of a non-symmetric matrix a bi-orthogonal algorithm is used.

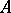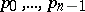If is symmetric and positive definite, then constructing an -orthogonal system by formula (1) with

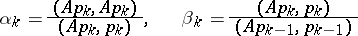enables one to avoid solving the auxiliary system (2) and gives an explicit expression for the coefficients 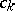: 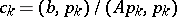. Here, to the method of -minimal iteration one can add the iteration

where . This modification of the method does not require a repeated use of all the vectors 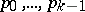. A minimal iteration method is used also for the solution of the complete eigen value problem and for finding the inverse matrix.

References

[1]	C. Lanczos, "An iteration method for the solution of the eigenvalue problem of linear differential and integral operators" Res. Nat. Bur. Stand. , 45 : 4 (1950) pp. 255–288
[2]	D.K. Faddeev, V.N. Faddeeva, "Computational methods of linear algebra" , Freeman (1963) (Translated from Russian)