Minimal iteration method
A method for solving linear algebraic equations 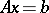 , in which the solution
, in which the solution  is represented as a linear combination of basis vectors which are orthogonal in some metric connected with the matrix of the system.
is represented as a linear combination of basis vectors which are orthogonal in some metric connected with the matrix of the system.
In the case of a symmetric matrix  , the orthogonal system of vectors
, the orthogonal system of vectors 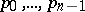 is constructed using the three-term recurrence formula
is constructed using the three-term recurrence formula
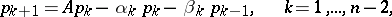 | (1) |
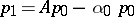 ,
, 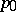 an arbitrary vector, where
an arbitrary vector, where
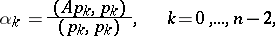 |
 |
The solution of the system 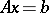 is found by the formula
is found by the formula 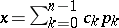 , and the coefficients
, and the coefficients 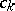 are given as the solutions of the system
are given as the solutions of the system
 | (2) |
If the orthogonalization algorithm is degenerate, that is, if 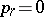 for
for  , one has to choose a new initial vector
, one has to choose a new initial vector 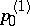 , orthogonal to
, orthogonal to  and one has to complete the system of basis vectors to a complete system.
and one has to complete the system of basis vectors to a complete system.
In the case of a non-symmetric matrix a bi-orthogonal algorithm is used.
If 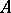 is symmetric and positive definite, then constructing an
is symmetric and positive definite, then constructing an  -orthogonal system
-orthogonal system 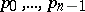 by formula (1) with
by formula (1) with
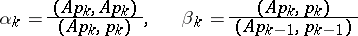 |
enables one to avoid solving the auxiliary system (2) and gives an explicit expression for the coefficients 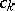 :
: 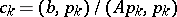 . Here, to the method of
. Here, to the method of  -minimal iteration one can add the iteration
-minimal iteration one can add the iteration
 |
where  . This modification of the method does not require a repeated use of all the vectors
. This modification of the method does not require a repeated use of all the vectors 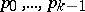 . A minimal iteration method is used also for the solution of the complete eigen value problem and for finding the inverse matrix.
. A minimal iteration method is used also for the solution of the complete eigen value problem and for finding the inverse matrix.
References
| [1] | C. Lanczos, "An iteration method for the solution of the eigenvalue problem of linear differential and integral operators" Res. Nat. Bur. Stand. , 45 : 4 (1950) pp. 255–288 |
| [2] | D.K. Faddeev, V.N. Faddeeva, "Computational methods of linear algebra" , Freeman (1963) (Translated from Russian) |
Minimal iteration method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Minimal_iteration_method&oldid=16741