Maximum and minimum points
Points in the domain of definition of a real-valued function at which it takes its greatest and smallest values; such points are also called absolute maximum and absolute minimum points. If 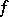 is defined on a topological space
is defined on a topological space 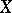 , then a point
, then a point 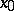 is called a local maximum (local minimum) point if there is a neighbourhood
is called a local maximum (local minimum) point if there is a neighbourhood 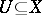 of
of  such that
such that  is an absolute maximum (minimum) point for the restriction of
is an absolute maximum (minimum) point for the restriction of 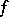 to this neighbourhood. One distinguishes between strict and non-strict maximum (minimum) points (both absolute and local). For example, a point
to this neighbourhood. One distinguishes between strict and non-strict maximum (minimum) points (both absolute and local). For example, a point 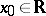 is called a non-strict (strict) local maximum point of
is called a non-strict (strict) local maximum point of 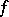 if there is a neighbourhood
if there is a neighbourhood 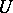 of
of 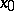 such that for all
such that for all 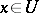 ,
, 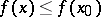 (
(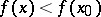 ,
, 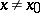 ).
).
For functions defined on finite-dimensional domains there are conditions and tests, in terms of differential calculus, for a given point to be a local maximum (minimum) point. Let 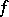 be defined in a neighbourhood of a point
be defined in a neighbourhood of a point 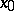 of the real line. If
of the real line. If  is a non-strict local maximum (minimum) point and if the derivative
is a non-strict local maximum (minimum) point and if the derivative 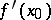 exists, then the latter is equal to zero.
exists, then the latter is equal to zero.
If a function 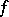 is differentiable in a neighbourhood of
is differentiable in a neighbourhood of 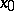 except, possibly, at
except, possibly, at 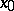 itself where it is continuous, and if the derivative
itself where it is continuous, and if the derivative 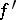 is of constant sign on each side of
is of constant sign on each side of 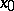 in this neighbourhood, then for
in this neighbourhood, then for 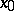 to be a strict local maximum (local minimum) point it is necessary and sufficient that the derivative changes sign from plus to minus, that is,
to be a strict local maximum (local minimum) point it is necessary and sufficient that the derivative changes sign from plus to minus, that is, 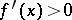 for
for  and
and 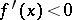 for
for 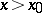 (respectively, from minus to plus;
(respectively, from minus to plus; 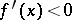 for
for 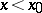 and
and 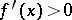 for
for  ). However, it is not possible to speak of the change of sign of the derivative at
). However, it is not possible to speak of the change of sign of the derivative at 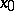 for every function
for every function 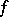 that is differentiable in a neighbourhood of
that is differentiable in a neighbourhood of 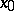 .
.
If 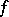 has
has 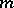 derivatives at
derivatives at 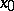 and if
and if 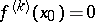 ,
, 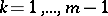 ,
, 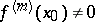 , then for
, then for  to be a strict local maximum point it is necessary and sufficient that
to be a strict local maximum point it is necessary and sufficient that 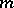 be even and that
be even and that 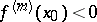 , and for a local minimum that
, and for a local minimum that 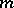 be even and
be even and 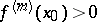 .
.
Let 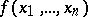 be defined in an
be defined in an  -dimensional neighbourhood of a point
-dimensional neighbourhood of a point  and let it be differentiable at this point. If
and let it be differentiable at this point. If 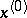 is a non-strict local maximum (minimum) point, then the differential of
is a non-strict local maximum (minimum) point, then the differential of 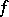 at this point is equal to zero. This condition is equivalent to all first-order partial derivatives of
at this point is equal to zero. This condition is equivalent to all first-order partial derivatives of 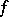 being zero at this point. If the function has continuous second-order partial derivatives at
being zero at this point. If the function has continuous second-order partial derivatives at 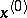 , if all its first-order derivatives are equal to zero at
, if all its first-order derivatives are equal to zero at 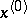 , and if the second-order differential at
, and if the second-order differential at  is a negative-definite (positive-definite) quadratic form, then
is a negative-definite (positive-definite) quadratic form, then  is a strict local maximum (minimum) point. Conditions for maximum and minimum points of differentiable functions are known when restrictions are imposed on the variation of the arguments in the domain: coupling equations must be satisfied. Necessary and sufficient conditions for a maximum (minimum) of a real-valued function with a more complicated structure of its domain of definition have been obtained in special areas of mathematics; for example, in convex analysis and mathematical programming (see also Maximization and minimization of functions). Maximum and minimum points of functions on manifolds are studied in variational calculus in the large, and maximum and minimum points for functions on function spaces, that is, for functionals, are studied in variational calculus. There are also various numerical approximation methods for finding maximum and minimum points.
is a strict local maximum (minimum) point. Conditions for maximum and minimum points of differentiable functions are known when restrictions are imposed on the variation of the arguments in the domain: coupling equations must be satisfied. Necessary and sufficient conditions for a maximum (minimum) of a real-valued function with a more complicated structure of its domain of definition have been obtained in special areas of mathematics; for example, in convex analysis and mathematical programming (see also Maximization and minimization of functions). Maximum and minimum points of functions on manifolds are studied in variational calculus in the large, and maximum and minimum points for functions on function spaces, that is, for functionals, are studied in variational calculus. There are also various numerical approximation methods for finding maximum and minimum points.
References
| [1] | V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , 1 , MIR (1982) (Translated from Russian) |
| [2] | L.D. Kudryavtsev, "A course in mathematical analysis" , 1–2 , Moscow (1981) (In Russian) |
| [3] | S.M. Nikol'skii, "A course of mathematical analysis" , 1 , MIR (1977) (Translated from Russian) |
| [4] | N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , MIR (1977) (Translated from Russian) |
Comments
References
| [a1] | K.R. Stromberg, "Introduction to classical real analysis" , Wadsworth (1981) |
Maximum and minimum points. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximum_and_minimum_points&oldid=47806