Mathieu equation
The following ordinary differential equation with real coefficients:
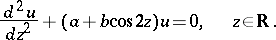 |
It was introduced by E. Mathieu [1] in the investigation of the oscillations of an elliptic membrane; it is a particular case of a Hill equation.
A fundamental system of solutions of the Mathieu equation has the form
 | (*) |
for 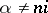 ,
,  an integer, where
an integer, where 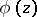 is a
is a 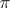 -periodic function and the Lyapunov characteristic exponent
-periodic function and the Lyapunov characteristic exponent 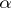 is either real or purely imaginary. For
is either real or purely imaginary. For  one of the solutions grows unboundedly, whereas the other tends to zero as
one of the solutions grows unboundedly, whereas the other tends to zero as 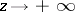 (instability zones in the plane of the parameters
(instability zones in the plane of the parameters 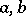 ); for
); for 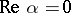 these solutions are both bounded (stability zones). On the boundary of these zones (the case excluded in (*)) one of the functions of the fundamental system of solutions is either
these solutions are both bounded (stability zones). On the boundary of these zones (the case excluded in (*)) one of the functions of the fundamental system of solutions is either 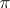 -periodic or
-periodic or  -periodic (the latter is called a Mathieu function, cf. Mathieu functions), while the second is obtained from the first through multiplication by
-periodic (the latter is called a Mathieu function, cf. Mathieu functions), while the second is obtained from the first through multiplication by  . The instability zones have the form of curvilinear triangles with vertices at the points
. The instability zones have the form of curvilinear triangles with vertices at the points  ,
,  ,
, 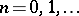 (see [2], [4]).
(see [2], [4]).
The Mathieu equation is known also in a different form (see [3]).
References
| [1] | E. Mathieu, "Course de physique mathématique" , Paris (1873) |
| [2] | M.J.O. Strett, "Lamésche-, Mathieusche- und verwandte Funktionen in Physik und Technik" , Springer (1932) |
| [3] | E. Kamke, "Differentialgleichungen: Lösungen und Lösungsmethoden" , 1. Gewöhnliche Differentialgleichungen , Chelsea, reprint (1971) |
| [4] | V.A. Yakubovich, V.M. Starzhinskii, "Linear differential equations with periodic coefficients and their applications" , 1–2 , Wiley (1975) (Translated from Russian) |
Comments
The operator involved in the Mathieu equation is called a Mathieu operator. In various applications, especially in solid state theory, a discrete analogue, the discrete Mathieu operator, defined by
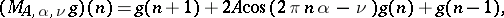 |
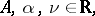 |
is important. If 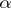 is rational this is a periodic operator, otherwise it is almost periodic. Let
is rational this is a periodic operator, otherwise it is almost periodic. Let 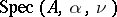 be the spectrum of
be the spectrum of 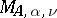 on
on 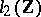 and let
and let
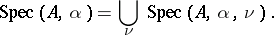 |
The spectrum 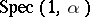 as a function of
as a function of 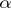 gives a figure in the plane with remarkable combinatorial regularity and Cantor set like properties. It is known as Hofstadter's butterfly [a1]. M. Kac conjectured (the Martini problem) that
gives a figure in the plane with remarkable combinatorial regularity and Cantor set like properties. It is known as Hofstadter's butterfly [a1]. M. Kac conjectured (the Martini problem) that 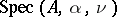 is a Cantor set for all irrational
is a Cantor set for all irrational 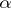 ,
, 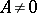 ,
,  ; another conjecture states that the Lebesgue measure of
; another conjecture states that the Lebesgue measure of 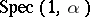 is zero for all irrational
is zero for all irrational 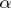 . For some detailed results on these spectra for rational
. For some detailed results on these spectra for rational 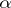 and a survey of this problem area cf. [a2]. A selection of noteworthy papers on these matters as well as results for the continuous analogues is [a3]–[a5].
and a survey of this problem area cf. [a2]. A selection of noteworthy papers on these matters as well as results for the continuous analogues is [a3]–[a5].
References
| [a1] | D. Hofstadter, "The energy levels of Bloch electrons in rational and irrational magnetic fields" Phys. Rev. , B14 (1976) pp. 2239–2249 |
| [a2] | P.M.M. van Mouché, "Sur les régions interdites du spectre de l'opérateur périodique et discret de Mathieu" , Math. Inst. Univ. Utrecht (1988) (Thesis) |
| [a3] | J. Bélissard, B. Simon, "Cantor spectrum for the almost Mathieu potential" J. Funct. Anal. , 48 (1982) pp. 408–419 |
| [a4] | J. Bélissard, R. Lima, D. Testarel, "Almost periodic Schrödinger operators" L. Streit (ed.) , Mathematics and Physics, lectures on recent results , 1 , World Sci. (1985) pp. 1–64 |
| [a5] | B. Simon, "Almost periodic Schrödinger operators, a review" Adv. Appl. Math. , 3 (1982) pp. 463–490 |
| [a6] | J. Meixner, F.W. Schäfke, "Mathieu functions and spheroidal functions and their mathematical foundations: further studies" , Springer (1980) |
Mathieu equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mathieu_equation&oldid=47790