Luzin sieve

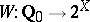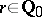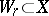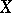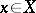An arbitrary mapping that puts each dyadic fraction into correspondence with a subset . As a rule, is assumed to be a complete separable metric space. It was introduced by N.N. Luzin [1]. The set of points such that there is an infinite sequence 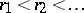that satisfies the condition 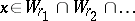is said to be sifted through the Luzin sieve 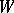. For every 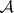-operation there is a Luzin sieve 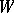such that the result of this 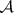-operation is sifted through 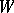. The main result concerning the Luzin sieve is that a Luzin set of the -th class (or of the projective class 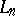) is invariant under the operation of sifting through the Luzin sieve for .

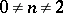References

[1]	N.N. Luzin, "Sur les ensembles analytiques" Fund. Math. , 10 (1927) pp. 1–95
[2]	C. Kuratowski, "Topology" , 1 , PWN & Acad. Press (1966) (Translated from French)

Comments

A Luzin set in the sense of the article is invariably called a projective set in the West. The Luzin sieve has been an extremely powerful tool in descriptive set theory; it gave rise, with other techniques, to the modern use of countable ordinals in this theory. For more details and references see Descriptive set theory.

This notion has nothing to do with the notion of sieve used by N. Bourbaki [a1] while proving one of the Luzin theorems. A Bourbaki sieve is just a way to write a disjoint Suslin scheme.

If 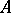is an analytic set and 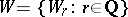is a Luzin sieve for 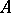consisting of closed sets, then, as one readily sees, 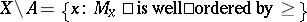, where 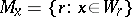. The sets 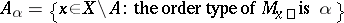, where 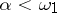, are called the constituents of the set 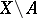determined by the sieve .

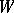References

[a1]	N. Bourbaki, "Elements of mathematics. General topology" , Addison-Wesley (1966) pp. Chapt. 10 (Translated from French)