Localization in a commutative algebra

A transition from a commutative ring to the ring of fractions (cf. Fractions, ring of) , where is a subset of . The ring can be defined as the solution of the problem of a universal mapping from into a ring under which all elements of become invertible. However, there are explicit constructions for :

1) as the set of fractions of the form , where 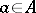and is a product of elements of 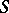(two fractions 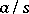and 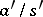are regarded as equivalent if and only if there is an 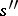that is a product of elements of 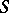and is such that 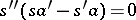; fractions are added and multiplied by the usual rules);

2) as the quotient ring of the ring of polynom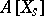ials , , with respect to the ideal generated by the polynomials , ;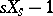

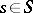3) as the inductive limit of an inductive system of 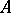-modules , where 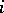runs through a naturally-ordered free commutative monoid 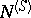. All the 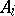are isomorphic to 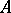, and the homomorphisms 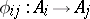with 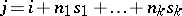coincide with multiplication by .

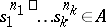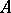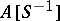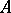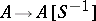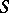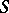The ring is canonically mapped into and converts the latter into an -algebra. This mapping is injective if and only if does not contain any divisor of zero in . On the other hand, if contains a nilpotent element, then .

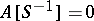Without loss of generality the set 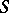can be assumed to be closed with respect to products (such a set is known as multiplicative, or as a multiplicative system). In this case the ring 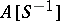is also denoted by or 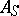. The most important examples of multiplicative systems are the following:

a) the set 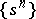of all powers of an element of ;

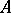b) the set 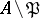, that is, the complement of a prime ideal 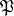. The corresponding ring of fractions is local and is denoted by ;

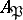c) the set 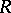of all non-divisors of zero in .

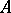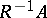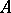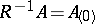The ring is called the complete ring of fractions of . If is integral, then is a field of fractions.

The operation of localization carries over with no difficulty to arbitrary -modules if one sets

The transition from to 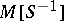is an exact functor. In other words, the 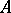-module is flat. Localization commutes with direct sums and inductive limits.

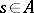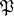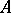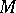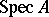From the geometrical point of view localization means transition to an open subset. More precisely, for the spectrum is canonically identified with the open (in the Zariski topology) subset consisting of the prime ideals not containing . Moreover, this operation makes it possible to associate with each -module a quasi-coherent sheaf on the affine scheme for which

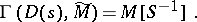Localization can be regarded as an operation that makes it possible to invert morphisms of multiplication by an 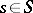in the category of -modules. In this approach the operation of localization admits a wide generalization to arbitrary categories (see Localization in categories).

References

[1]	N. Bourbaki, "Elements of mathematics. Commutative algebra" , Addison-Wesley (1972) (Translated from French)