Lie ternary system

A vector space 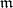with a trilinear composition

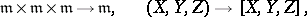satisfying the following conditions:

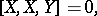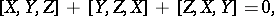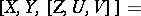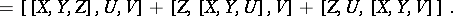If 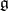is a Lie algebra and 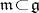is a subspace such that 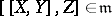for any 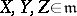, then the operation

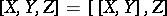converts 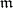into a Lie ternary system. Conversely, every Lie ternary system can be obtained in this way from some Lie algebra.

The category of finite-dimensional Lie ternary systems over the field 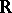is equivalent to the category of simply-connected symmetric homogeneous spaces (see Symmetric space).

References

[1]	S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978)
[2]	O. Loos, "Symmetric spaces" , 1 , Benjamin (1969)