Leray formula
Cauchy–Fantappié formula
A formula for the integral representation of holomorphic functions  of several complex variables
of several complex variables 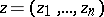 ,
, 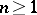 , which generalizes the Cauchy integral formula (see Cauchy integral).
, which generalizes the Cauchy integral formula (see Cauchy integral).
Let 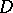 be a finite domain in the complex space
be a finite domain in the complex space  with piecewise-smooth boundary
with piecewise-smooth boundary 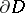 and let
and let  be a smooth vector-valued function of
be a smooth vector-valued function of 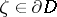 with values in
with values in 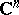 such that the scalar product
such that the scalar product
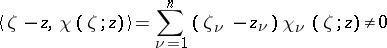 |
everywhere on  for all
for all 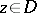 . Then any function
. Then any function 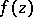 holomorphic in
holomorphic in 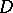 and continuous in the closed domain
and continuous in the closed domain 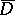 can be represented in the form
can be represented in the form
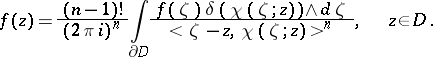 | (*) |
Formula (*) generalizes Cauchy's classical integral formula for analytic functions of one complex variable and is called the Leray formula. J. Leray, who obtained this formula (see [1]), called it the Cauchy–Fantappié formula. In this formula the differential forms 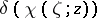 and
and 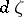 are constituted according to the laws:
are constituted according to the laws:
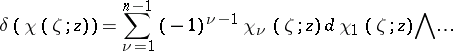 |
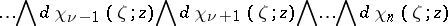 |
and
 |
where 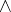 is the sign of exterior multiplication (see Exterior product). By varying the form of the function
is the sign of exterior multiplication (see Exterior product). By varying the form of the function 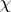 it is possible to obtain various integral representations from formula (*). One should bear in mind that, generally speaking, the Leray integral in (*) is not identically zero when
it is possible to obtain various integral representations from formula (*). One should bear in mind that, generally speaking, the Leray integral in (*) is not identically zero when  is outside
is outside 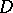 .
.
See also Bochner–Martinelli representation formula.
References
| [1] | J. Leray, "Le calcul différentielle et intégrale sur une variété analytique complexe" Bull. Soc. Math. France , 87 (1959) pp. 81–180 |
| [2] | B.V. Shabat, "Introduction of complex analysis" , 2 , Moscow (1976) (In Russian) |
Comments
Often the Leray formula is understood to be a more general representation formula, valid for arbitrary sufficiently smooth (e.g., 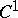 ) functions on a domain
) functions on a domain 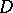 in
in 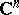 . Let
. Let 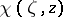 ,
, 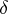 and
and 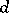 be as defined above,
be as defined above, 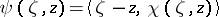 . Furthermore, define for
. Furthermore, define for  ,
,  and
and 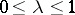 :
:
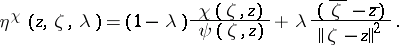 |
Let 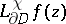 denote the right-hand side of (*). It is well defined for measurable functions
denote the right-hand side of (*). It is well defined for measurable functions 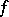 on
on 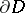 . Define for a continuous
. Define for a continuous  -form
-form  on
on 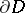 ,
,
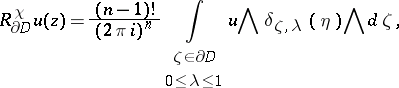 |
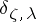 meaning that the exterior derivative in the definition of
meaning that the exterior derivative in the definition of 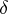 has to be with respect to
has to be with respect to  as well as
as well as 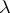 . Next, for
. Next, for 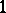 -forms
-forms  defined on
defined on 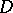 there holds
there holds
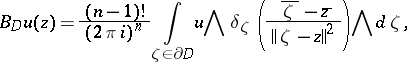 |
the Bochner–Martinelli operator.
Now let 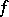 be a continuous function on
be a continuous function on 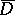 such that
such that 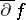 is continuous there too. Then Leray's formula reads
is continuous there too. Then Leray's formula reads
 | (a1) |
where 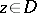 .
.
If  is holomorphic on
is holomorphic on 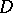 , then (a1) reduces to (*). Of particular importance are instances where
, then (a1) reduces to (*). Of particular importance are instances where 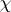 , and hence also
, and hence also 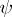 , is holomorphic as a function of
, is holomorphic as a function of  for
for 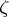 fixed — this can only occur if
fixed — this can only occur if 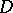 is pseudo-convex;
is pseudo-convex; 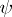 is then a holomorphic support function (i.e. for all
is then a holomorphic support function (i.e. for all 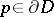 there is a neighbourhood
there is a neighbourhood 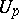 of
of 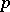 such that
such that 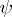 is holomorphic in this neighbourhood and
is holomorphic in this neighbourhood and  ), the existence of which is closely related to the existence of continuously varying holomorphic peaking functions. (A continuously varying holomorphic peaking function for
), the existence of which is closely related to the existence of continuously varying holomorphic peaking functions. (A continuously varying holomorphic peaking function for 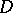 is a function
is a function 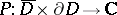 such that for each fixed
such that for each fixed 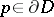 : 1)
: 1) 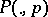 is holomorphic on
is holomorphic on 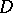 and continuous on
and continuous on 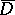 ; and 2)
; and 2) 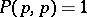 and
and 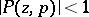 for all
for all 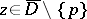 . If
. If 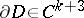 ,
,  is required to be
is required to be 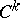 for each fixed
for each fixed 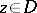 .) Then
.) Then 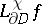 is holomorphic for every continuous
is holomorphic for every continuous 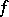 on
on 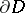 and the operator
and the operator
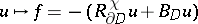 |
solves the inhomogeneous Cauchy–Riemann equations
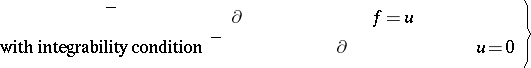 | (a2) |
for continuous 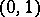 -forms
-forms  on
on 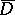 . Formula (a1) can be generalized to give a representation formula for
. Formula (a1) can be generalized to give a representation formula for 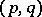 -forms as well (see [a2]).
-forms as well (see [a2]).
Thus, the Leray formula has become an important tool for solving the Levi problem (work of G.M. Khenkin [a1] and of E. Ramirez de Arellano [a3]) and for obtaining estimates for solutions of (a2). In particular, the following sharp Hölder estimates hold on strictly pseudo-convex domains: There is a solution 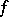 with
with  , where
, where 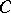 depends on the domain only,
depends on the domain only, 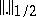 denotes the Hölder
denotes the Hölder 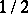 -norm and
-norm and 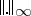 denotes the sup-norm. Many analysts made contributions in this direction, notably Khenkin and A.V. Romanov; H. Grauert and I. Lieb; and N. Kerzman and R.M. Range.
denotes the sup-norm. Many analysts made contributions in this direction, notably Khenkin and A.V. Romanov; H. Grauert and I. Lieb; and N. Kerzman and R.M. Range.
References
| [a1] | G.M. [G.M. Khenkin] Henkin, "Integral representations of functions holomorphic in strictly pseudoconvex domains and some applications" Math. USSR Sb. , 78 (1969) pp. 611–632 Mat. Sb. , 7 (1969) pp. 597–616 |
| [a2] | J.L. Leiterer, "Theory of functions on complex manifolds" , Birkhäuser (1984) |
| [a3] | E. Ramirez de Arellano, "Ein Divisionsproblem und Randintegraldarstellungen in der komplexen Analysis" Math. Ann. , 184 (1970) pp. 172–187 |
| [a4] | R.M. Range, "Holomorphic functions and integral representation in several complex variables" , Springer (1986) pp. Chapt. VI, Par. 6 |
Leray formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Leray_formula&oldid=47615