One of the fundamental problems in the classical calculus of variations. It consists in minimizing the functional
in the presence of differential constraints of equality type:
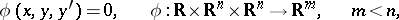 | (1) |
and boundary conditions
The Lagrange problem is usually considered under the condition that the system (1) is regular, that is, the matrix 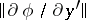 has maximal rank:
has maximal rank:
Under this condition the system (1) can be solved for part of the variables and, using a different notation ( instead of
instead of  ), the Lagrange problem can be reduced to the form
), the Lagrange problem can be reduced to the form
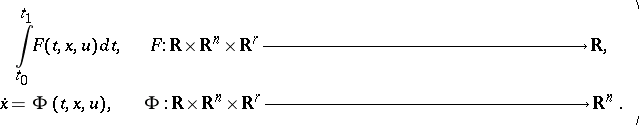 | (2) |
The function 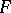 and the mapping
and the mapping 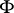 are usually assumed to be continuously differentiable. Problems of optimal control are often specified in the form (2) (the Pontryagin form), and restrictions are, moreover, imposed on the control
are usually assumed to be continuously differentiable. Problems of optimal control are often specified in the form (2) (the Pontryagin form), and restrictions are, moreover, imposed on the control 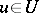 . Necessary conditions for a strong extremum for the problem (2) (for simplicity, with fixed left-hand end
. Necessary conditions for a strong extremum for the problem (2) (for simplicity, with fixed left-hand end 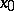 and free right-hand end
and free right-hand end 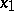 ) have the following form. Let
) have the following form. Let
be the Lagrange function. For a vector function 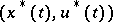 to be a strong minimum in the Lagrange problem (2) it is necessary that the following relations hold:
to be a strong minimum in the Lagrange problem (2) it is necessary that the following relations hold:
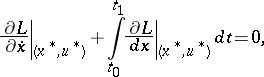 | (3) |
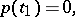 | (4) |
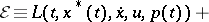 | (5) |
for all possible admissible values of 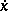 and
and  .
.
If one carries out differentiation in (3) with respect to 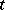 and uses the notation
and uses the notation
then a necessary condition for a strong minimum can be stated in the form of a maximum principle, in which the Euler equation (3), the transversality condition (4) and the Weierstrass condition (5) are combined. For a vector function 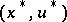 to be a strong minimum in the problem (2) with fixed left-hand end and free right-hand end it is necessary that there is a solution of the system
to be a strong minimum in the problem (2) with fixed left-hand end and free right-hand end it is necessary that there is a solution of the system
for which
J.L. Lagrange considered similar problems in connection with studies in mechanics (in the second half of the 18th century).
For references see Variational calculus.
The notation 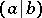 denotes the inner product of the vectors
denotes the inner product of the vectors  and
and 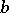 .
.
How to Cite This Entry:
Lagrange problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lagrange_problem&oldid=47559
This article was adapted from an original article by I.B. VapnyarskiiV.M. Tikhomirov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article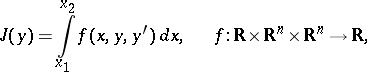
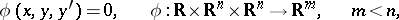

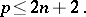
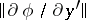 has maximal rank:
has maximal rank:
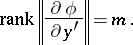
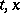 instead of
instead of 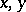 ), the Lagrange problem can be reduced to the form
), the Lagrange problem can be reduced to the form
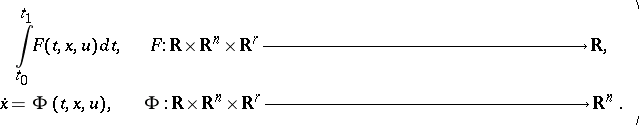
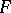 and the mapping
and the mapping 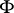 are usually assumed to be continuously differentiable. Problems of optimal control are often specified in the form (2) (the Pontryagin form), and restrictions are, moreover, imposed on the control
are usually assumed to be continuously differentiable. Problems of optimal control are often specified in the form (2) (the Pontryagin form), and restrictions are, moreover, imposed on the control 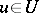 . Necessary conditions for a strong extremum for the problem (2) (for simplicity, with fixed left-hand end
. Necessary conditions for a strong extremum for the problem (2) (for simplicity, with fixed left-hand end 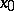 and free right-hand end
and free right-hand end 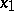 ) have the following form. Let
) have the following form. Let
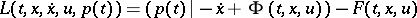
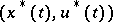 to be a strong minimum in the Lagrange problem (2) it is necessary that the following relations hold:
to be a strong minimum in the Lagrange problem (2) it is necessary that the following relations hold:
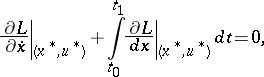
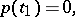
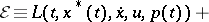
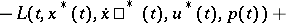
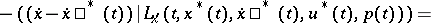
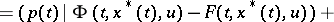
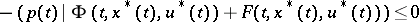
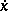 and
and  .
.
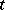 and uses the notation
and uses the notation
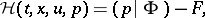
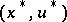 to be a strong minimum in the problem (2) with fixed left-hand end and free right-hand end it is necessary that there is a solution of the system
to be a strong minimum in the problem (2) with fixed left-hand end and free right-hand end it is necessary that there is a solution of the system
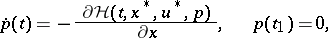
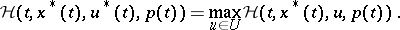
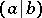 denotes the inner product of the vectors
denotes the inner product of the vectors  and
and 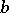 .
.