Kellogg theorem

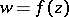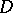Let be a function realizing a univalent conformal mapping of the disc onto a domain bounded by a smooth closed Jordan curve 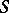for which the angle of inclination 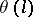of the tangent to the real axis, as a function of the arc length 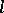of 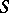, satisfies a Hölder condition:

Then the derivative is continuous in the closed disc 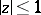, and on the circle the following Hölder conditions hold, with the same exponent :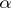

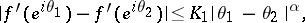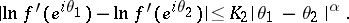Kellogg's theorem is a direct corollary of more general results by O.D. Kellogg (see [1], [2]) on the boundary behaviour of the partial derivatives of orders of a harmonic function that is a solution of the Dirichlet problem for a domain 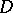in Euclidean space 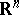, , 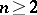bounded by a sufficiently-smooth Lyapunov surface 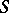(for 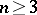) or a Lyapunov curve 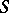(for 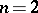; see Lyapunov surfaces and curves), where the given function 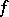is also assumed to be sufficiently smooth on the boundary .

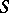Other results on the boundary behaviour of the derivative of the mapping function can be found in [3], [4].

References

[1]	O.D. Kellogg, "Harmonic functions and Green's integral" Trans. Amer. Math. Soc. , 13 : 1 (1912) pp. 109–132
[2]	O.D. Kellogg, "On the derivatives of harmonic functions on the boundary" Trans. Amer. Math. Soc. , 33 : 2 (1931) pp. 486–510
[3]	G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian)
[4]	S.E. Warschawski, "On differentiability at the boundary in conformal mapping" Proc. Amer. Math. Soc. , 12 (1961) pp. 614–620

Comments

See also Conformal mapping, boundary properties of a.

See [a1], p.15, for a similar problem.

References

[a1]	M. Brélot, "Eléments de la théorie classique du potentiel" , Sorbonne Univ. Centre Doc. Univ. , Paris (1959)