Jenkins theorem

general coefficient theorem

A theorem in the theory of univalent conformal mappings of families of domains on a Riemann surface, containing an inequality for the coefficients of the mapping functions, as well as conditions to be satisfied by the function so that the inequality becomes an equality. Jenkins' theorem is an exact expression and generalization of Teichmüller's principle (stated without proof, [1]), according to which the solution of a certain class of extremal problems for univalent functions is determined by the quadratic differentials of the respective forms. Obtained by J.A. Jenkins in 1954 [1]–[4].

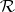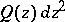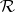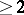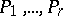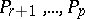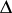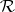The conditions of Jenkins' theorem. Let be a finite oriented Riemann surface, let be a positive quadratic differential on with at least one pole of order , and let be all the poles of order 2, while are all the poles of orders higher than 2. Let an open and everywhere-dense set on be the complement of the union of a finite number of closures of trajectories and closures of trajectory arcs, and let 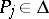, 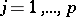. Suppose the function 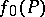maps 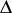conformally and univalently (cf. Conformal mapping) into 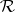, and suppose there exists a homotopy

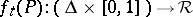of the mapping 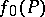into the identity mapping 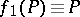which leaves all poles from 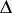fixed and satisfies the condition 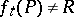for each pole 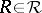, , 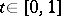and each poin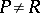t . Let 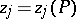be a local parameter for the pole 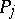such that 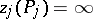, 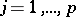. Let, for 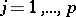, in a neighbourhood of the pole ,

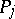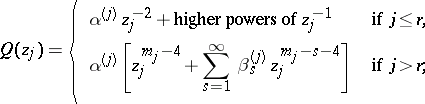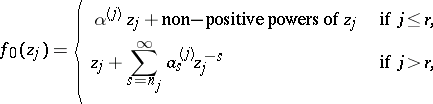where 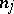is the integer part of the number 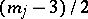. Let

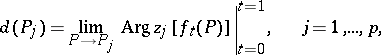and let 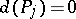for all 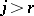for which 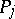lies on the boundary of a strip-like domain with respect to 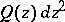. Finally, let

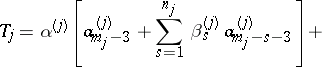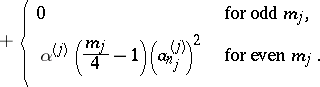The statement of Jenkins' theorem. Under the conditions mentioned above,

(*)

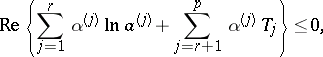where , .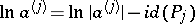

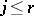Jenkins' theorem in the case of equality. If in (*) the equality sign holds, then: a) in each domain 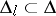the mapping 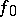is an isometry in the 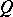-metric: 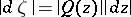, each trajectory 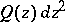in 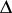is mapped to a trajectory, and the set is everywhere-dense in 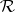; b) for 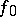to be the identity mapping in a certain domain 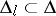it is sufficient that one of the following additional conditions holds:

1) 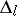contains a pole 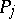, , 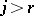of order 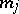such that 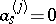for ;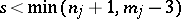

2) 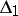contains a pole 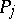for which 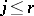and ;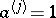

3) 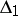contains a point of a trajectory ending in a simple pole.

If (*) is an equality and if 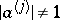for a certain 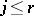, then 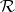is conformally equivalent to the sphere, 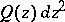has no zeros or simple poles and 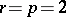. If, in addition, 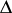is a domain, the mapping 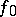is conformally equivalent to a linear mapping all fixed points of which are images of the poles.

The method of the extremal metric (cf. Extremal metric, method of the), on which the proof of Jenkins' theorem is based, was employed by Jenkins, with suitable modifications, to obtain several other results, in particular the so-called special coefficient theorem [4]. For additions to and the development of Jenkins' theorem, see [5].

References

[1]	J.A. Jenkins, "Univalent functions and conformal mapping" , Springer (1958)
[2]	J.A. Jenkins, "An extension of the general coefficient theorem" Trans. Amer. Math. Soc. , 95 : 3 (1960) pp. 387–407
[3]	J.A. Jenkins, "The general coefficient theorem and certain applications" Bull. Amer. Math. Soc. , 68 : 1 (1962) pp. 1–9
[4]	J.A. Jenkins, "Some area theorems and a special coefficient theorem" Illinois J. Math. , 8 : 1 (1964) pp. 80–99
[5]	P.M. Tamrazov, "On the general coefficient theorem" Math. USSR Sb. , 1 (1967) pp. 49–59 Mat. Sb. , 72 : 1 (1967) pp. 59–71